中学校3年生数学ｰ関数 y=ax2の変域
今日は関数y=ax2の変域の求め方について学習していくよ。
まずは次の問題について考えてみましょう。
まずは次の問題について考えてみましょう。
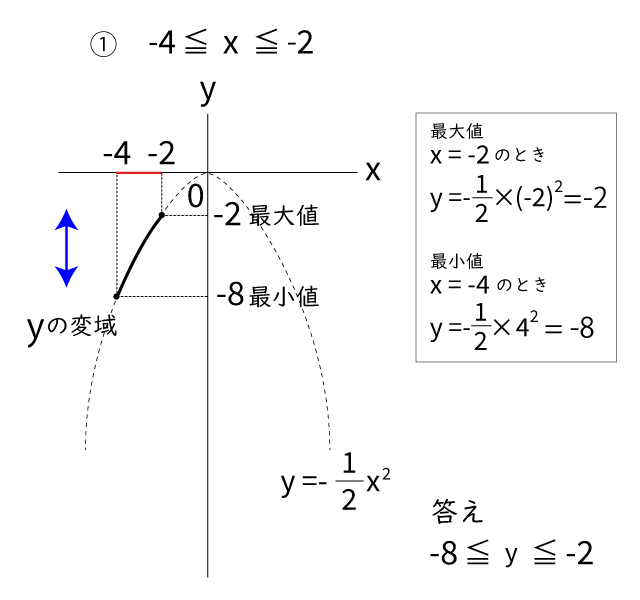
問題（1）
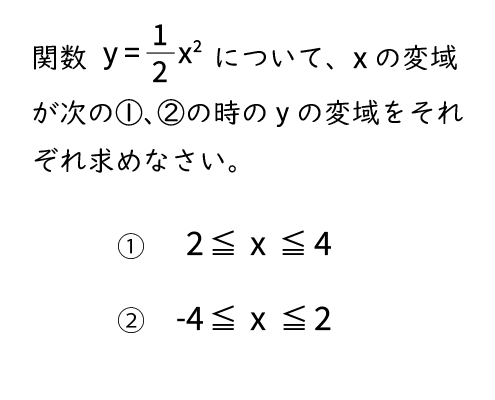
難しいなぁ。
変域の問題を解く際のポイントとか何かありませんか。
変域の問題を解く際のポイントとか何かありませんか。
変域の問題はグラフを利用して考えると分かりやすいですよ。
まずは簡単な放物線のグラフを書き、xの変域の部分で切り取ってみます。
その際、この関数は、a＞0なので上に開くグラフになることに注意しましょう。
そうすると、①、②のグラフは下のようになります。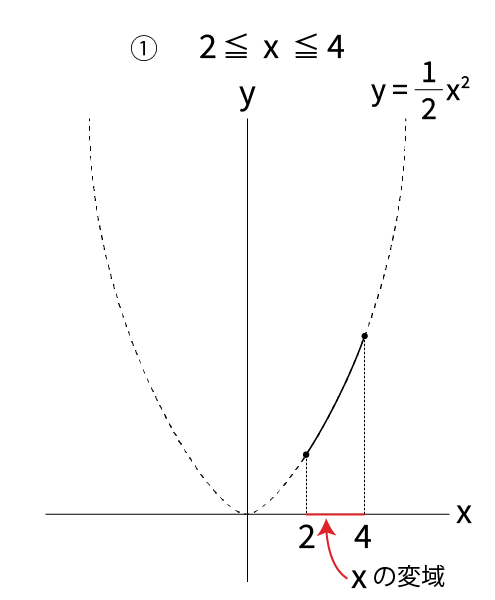
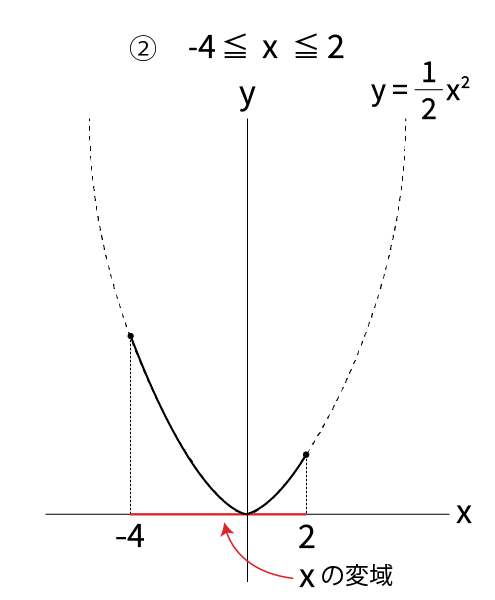
まずは簡単な放物線のグラフを書き、xの変域の部分で切り取ってみます。
その際、この関数は、a＞0なので上に開くグラフになることに注意しましょう。
そうすると、①、②のグラフは下のようになります。
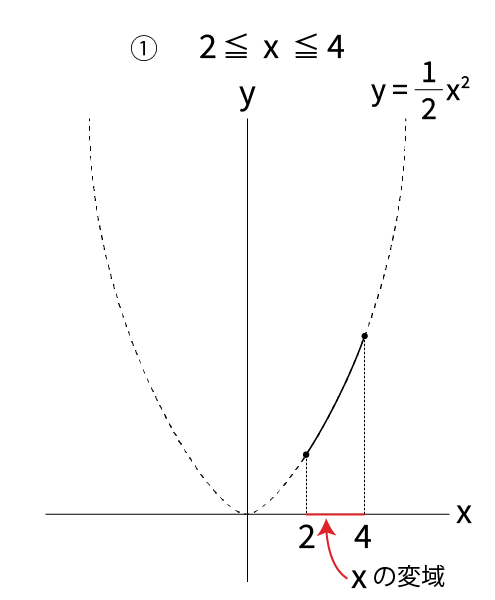
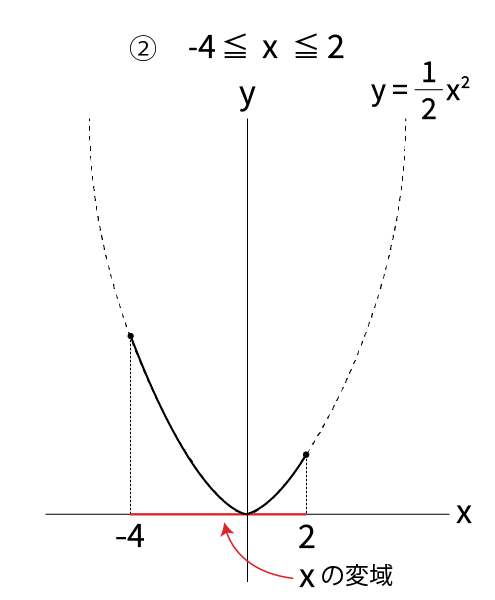
次にグラフを見ながらy=1/2 x2 の xに値を代入して、yの値の最大値と最小値を求めます。
最大値はグラフの1番高い所、最小値は１番低い所のyの値になります。
そして 最小値≦y≦最大値 がyの変域になります。
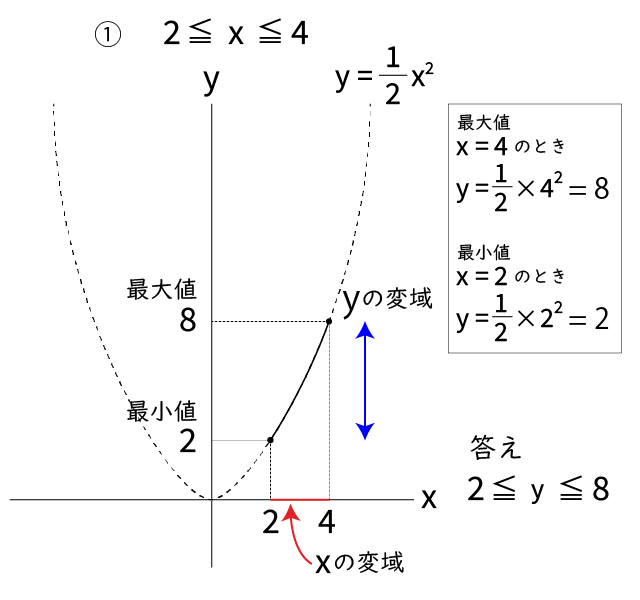
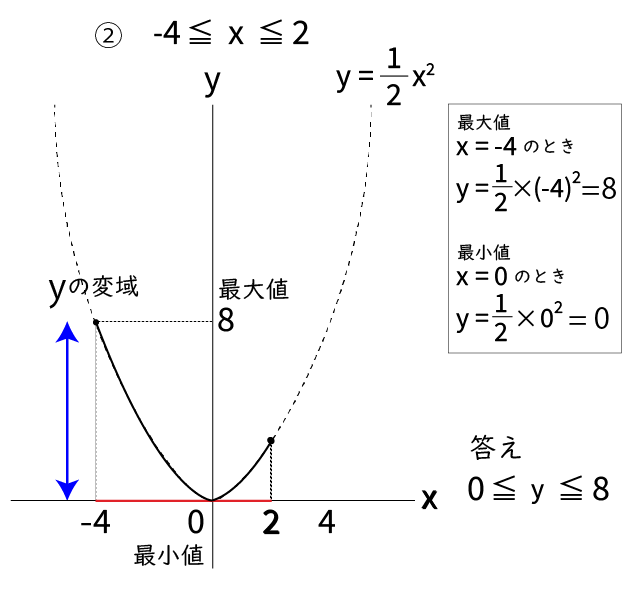
最大値はグラフの1番高い所、最小値は１番低い所のyの値になります。
そして 最小値≦y≦最大値 がyの変域になります。
②のようにxの変域に0が含まれるときは、最小値も0になるので注意が必要ですね。
その通りです。ではこれまでのポイントを踏まえて，もう１問解いてみましょう。
問題（2）
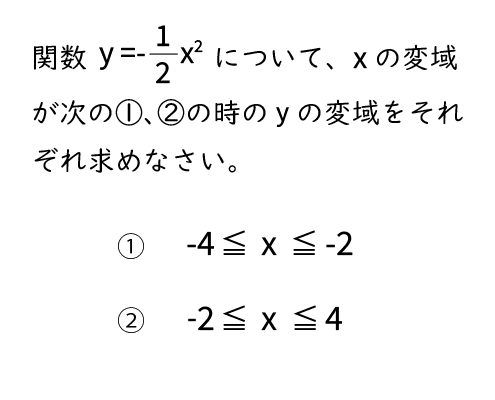
今度の関数はa＜0なので、下に開くグラフのようになります。
グラフと答えはそれぞれ下のようになります。
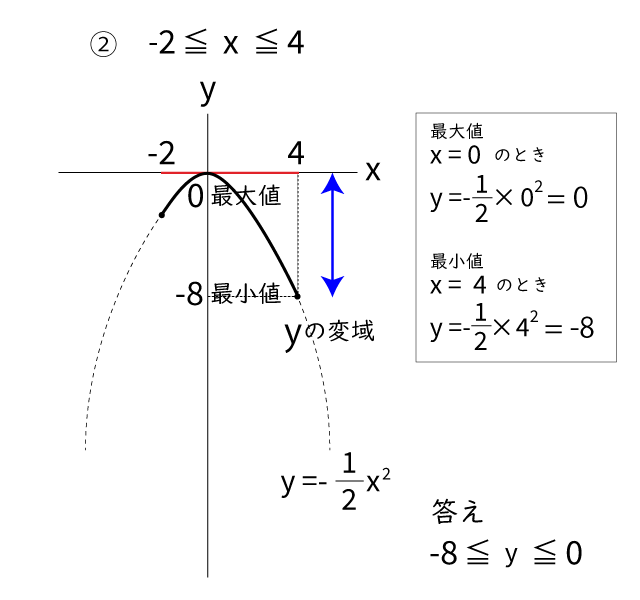
完璧です！よく出来ました。では次が最後の問題です。
問題（3）
関数 y=ax2で、xの変域が -1≦x≦3のときの yの変域が b≦y≦18である。
このとき、a、bの値をそれぞれ求めなさい。
このとき、a、bの値をそれぞれ求めなさい。
今度はaの値が分かっていないので、グラフが上・下どちらに開くのか分からないですね。
そうですね。こういったときは、yの変域の値に注目します。
b≦y≦18のように yの変域に正の数が含まれているときや、0≦y≦bのように最小値が0になっているときは、上に開くグラフになります。
反対に－3≦y≦bのように yの変域に負の数が含まれているときや、b≦y≦0のように最大値が0になっているときは下に開くグラフになります。
なるほど。この問題ではyの変域に正の数が含まれているので上に開くグラフになりますね。そうすると、グラフは下のようになります。
グラフを見るとx＝3のときy＝18となるので、y=ax^2に代入して計算するとa=2となります。また yの変域は0≦y≦18であることが分かるので、b=0です。
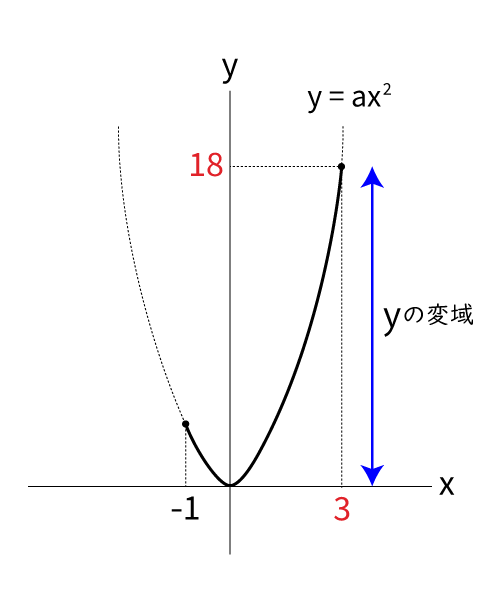
正解です！他にも変域の問題には色々なパターンがあるので、ぜひチャレンジしてみて下さい。
ITTO長野の中学生数学プラン
現在の学習状況と志望校をお伺いしながらプランはご案内しております。詳しくは各教室まで。例えばこんなプランで
ITTO長野の中学生数学プランのお問い合わせ
LINEで問い合わせ
※下のボタンをクリックして、お友達追加からお名前（フルネーム）とご用件をお送りください。