中学校1年生数学ｰおうぎ形（周の長さ）
単元：円とおうぎ
今日は，おうぎ形を使った問題に取り組んでいくよ。
いきなりだけど，この問題解けるかな？
問題：下の図の色をつけた部分の周の長さを求めなさい。
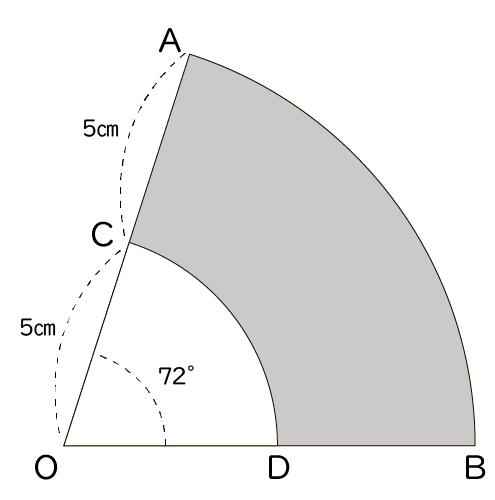
いきなりだけど，この問題解けるかな？
問題：下の図の色をつけた部分の周の長さを求めなさい。
先生！おうぎ形の弧の長さや面積の求め方は知ってるけど，こんなの習ってないよぉー(;´Д｀)
生徒くん、落ち着いて。今まで学習したことを使えば必ず求められますよ（^_^）まずは色のついた部分をペンで囲ってみましょう。
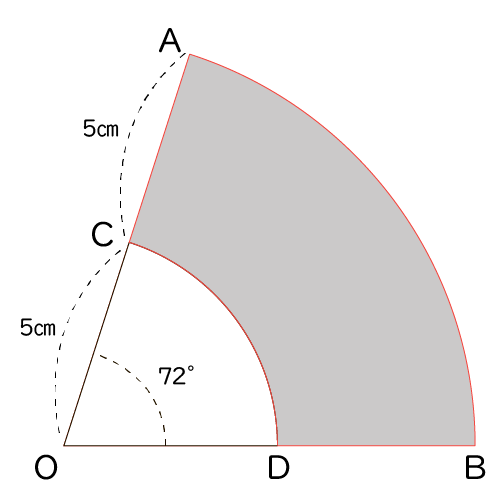
はい！囲いました！
OK！今囲った部分が周の長さになります。
つまり弧AB，CDと線分AC，BDの４つの長さの合計が周の長さということです。
つまり弧AB，CDと線分AC，BDの４つの長さの合計が周の長さということです。
なるほど！それなら求められるぞ！
弧ABは2π×10×72/360＝4π(cm)，
弧CDは2π×5×72/360＝2π(cm)，
線分AC，BDはそれぞれ5㎝だから，
周の長さは4π＋2π＋5＋5＝6π＋10(cm)ですね！
正解です!!よく出来ましたね!!
このように図形の周の長さは，弧や線分ごとに長さを求めて最後に合計すれば求めることができます。
ちなみ生徒くんはできていましたが，6π＋10はこれ以上簡単にはできないので16πとしないように注意しましょう！
ITTO長野の中学生数学プラン
現在の学習状況と志望校などをお伺いしながらプランはご案内しております。詳しくは各教室まで。例えばこんなプランで
ITTO長野の中学生数学プランのお問い合わせ
LINEで問い合わせ
※下のボタンをクリックして、お友達追加からお名前（フルネーム）とご用件をお送りください。