【中3】2次方程式の利用（道幅）
単元：2次方程式の利用問題
問題
下の図のように、縦の長さが15ｍ、横の長さが20ｍの長方形の土地に、同じ幅の通路が2本ある花壇を作ります。花壇の部分の面積150㎡になるようにするには、通路の幅を何ｍにすればよいですか。
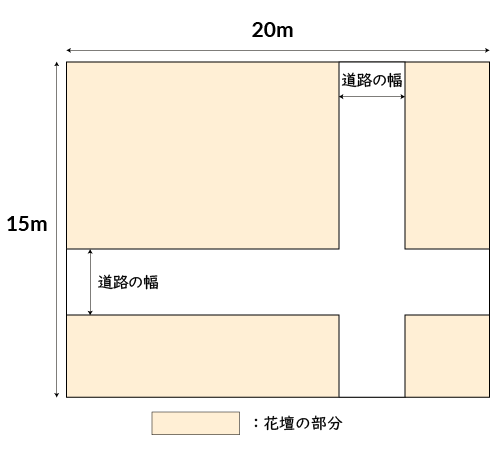
道路の幅をxｍとして考えてみましょう。
通路を下の図のように右端と下に動かし、花壇をひとまとまりにして考えるのがポイントです。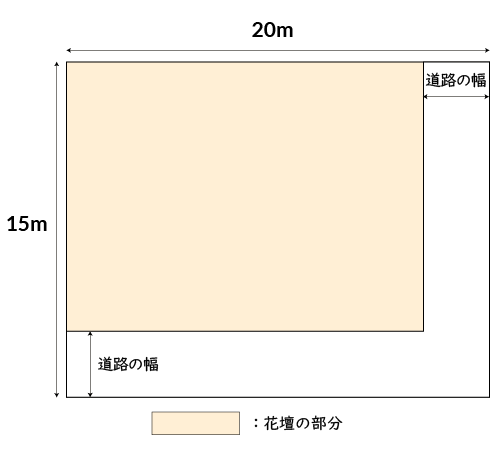
通路を下の図のように右端と下に動かし、花壇をひとまとまりにして考えるのがポイントです。
なるほど！通路を動かすと4つに分かれた花壇が一つにまとまって面積が出しやすそうです。
通路を動かしても、その面積は変わらないので、式を作りやすくします。
一つにまとまった花壇の縦の長さと横の長さをｘを使った式で表し、花壇の面積を求める等式を作ってみましょう。
一つにまとまった花壇の縦の長さと横の長さをｘを使った式で表し、花壇の面積を求める等式を作ってみましょう。
花壇の縦は、(15－x)m
花壇の横は、(20－x)mとなるので
花壇の面積＝縦×横＝(15－x)(20－ｘ)m2で
花壇の面積＝150m2だから
(15-x)(20-x)=150になります。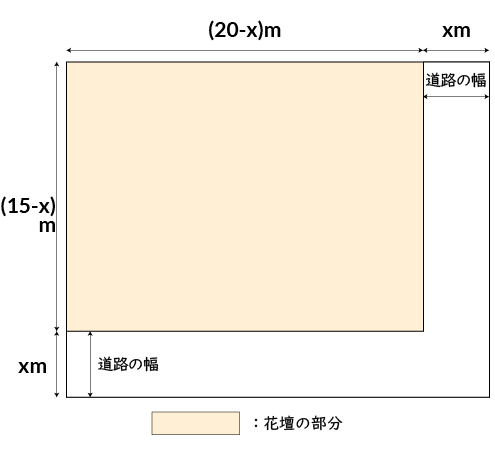
花壇の横は、(20－x)mとなるので
花壇の面積＝縦×横＝(15－x)(20－ｘ)m2で
花壇の面積＝150m2だから
(15-x)(20-x)=150になります。
OKです。それでは、作った方程式を解いてみましょう。
まずは左辺を展開すると良いです。
まずは左辺を展開すると良いです。
(15-x)(20-x)=150
300-35x+x2=150
x2-35x＋150＝0
因数分解をすると、
(x-3)(x-50)=0
x=3、50となります。2つ解が出たのですが、どちらとも解答になるのですか？
300-35x+x2=150
x2-35x＋150＝0
因数分解をすると、
(x-3)(x-50)=0
x=3、50となります。2つ解が出たのですが、どちらとも解答になるのですか？
良い質問です。通路の幅は元々の土地よりも広い幅で作ることはできません。
通路の幅が50ｍとすると、元の土地よりも広くなってしまいます。
通路の幅が50ｍとすると、元の土地よりも広くなってしまいます。
問題文をよく読むと、確かにそうですね！
答えは3mです。
答えは3mです。
よくできました。
2次方程式の利用問題では、その方程式の解が問題にあっていない場合があります。
解いた後には、解が問題にあっているかどうかを調べるようにしましょう。
2次方程式の利用問題では、その方程式の解が問題にあっていない場合があります。
解いた後には、解が問題にあっているかどうかを調べるようにしましょう。
ITTO長野の中学生数学プラン
現在の学習の状況と志望校をお伺いしながらプランのご案内をいたします。詳しくは各教室まで。例えばこんなプランで
ITTO長野の中学生数学プランのお問い合わせ
LINEからお問い合わせ
※下のボタンをクリックして、お友達追加からお名前（フルネーム）とご用件をお送りください。