中学校3年生数学 相似 線分比の問題
問題
下の図で四角形ABCDは、AD//BCの台形である。
辺AB上に点Eを取り。点Eを通って辺BCに平行な直線と辺CDとの交点をFとする。
AD＝3、EF＝8、BC＝11、EB＝6のとき、SEの長さを求めよ。
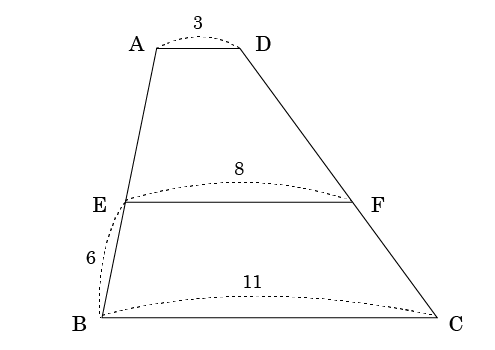
まずはじめに、相似となる図形ができるように、図の中に補助線を引き、相似となる図形を作ってみましょう。
Dを通る辺ABと平行になる補助線を引いて、辺EF、辺BCとの交点をそれぞれG、Hとすると、三角形DHGができて相似の図形が出来そうです。
OKです。それでは、△DGFと△DHCが相似になることを簡単に説明します。
GF//HCより、同位角はそれぞれ等しいので、
∠DGF＝∠DHC･･･（1）
∠DFG＝∠DCH･･･（2）
（1）、（2）より相似条件「2組の角がそれぞれ等しい」が成り立つので△DGF∽△DHCが証明できます。
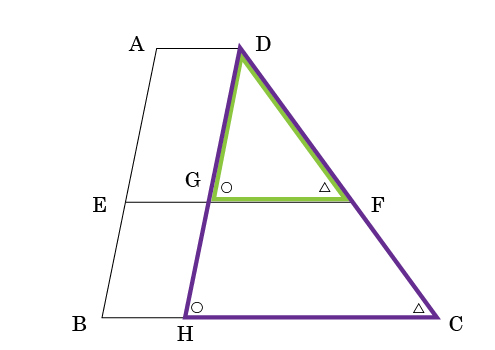それでは、その相似な図形から、DG、GH、GF、HCの長さの求め方を考えてみましょう。ヒントは、四角形ABHDは平行四辺形になります。
平行四辺形の向かい合う辺はそれぞれ等しいから、AD＝BHとなるので、AD＝BH＝3まではわかりましたが･･･。
そうすると四角形AEGDも平行四辺形となるので、AD＝EGとなるので、EG＝3も同様に言えます。
そうか！
EG＝3よりGF＝EFーEG＝8－3＝5
BH＝3よりHC＝BCーBH＝11ー3＝8、です。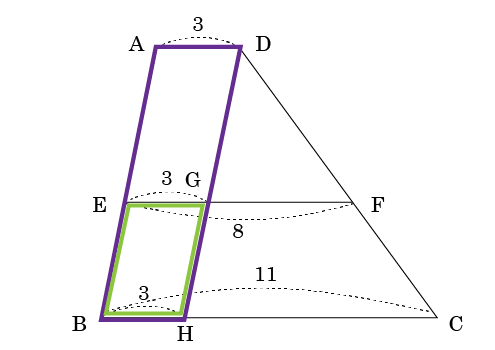
EG＝3よりGF＝EFーEG＝8－3＝5
BH＝3よりHC＝BCーBH＝11ー3＝8、です。
その通り！
それでは、AEをxとして残りの長さを考えてみましょう。
それでは、AEをxとして残りの長さを考えてみましょう。
四角形AEGDが平行四辺形だからAE＝DG＝x、
四角形EBHGも平行四辺形だからEB＝GH＝6までは、わかりました。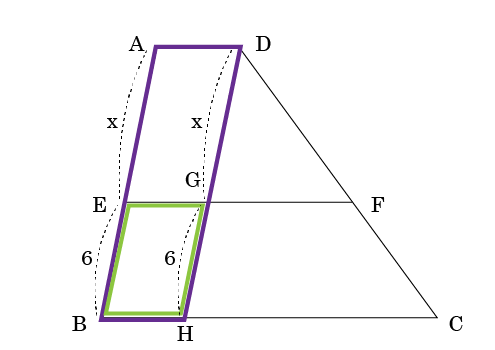
四角形EBHGも平行四辺形だからEB＝GH＝6までは、わかりました。
よくできました。
それでは、先ほど証明した△DGFち△DHCの相似比を使って考えてみましょう。
相似の比例式は以下のように対応する辺から作りましょう。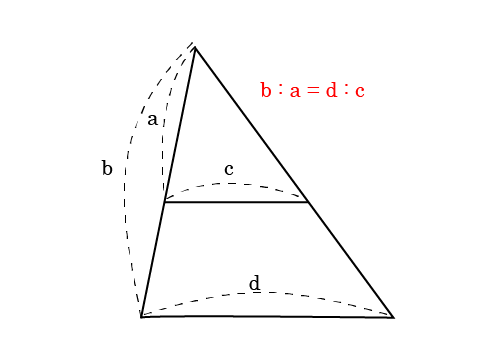
それでは、先ほど証明した△DGFち△DHCの相似比を使って考えてみましょう。
相似の比例式は以下のように対応する辺から作りましょう。
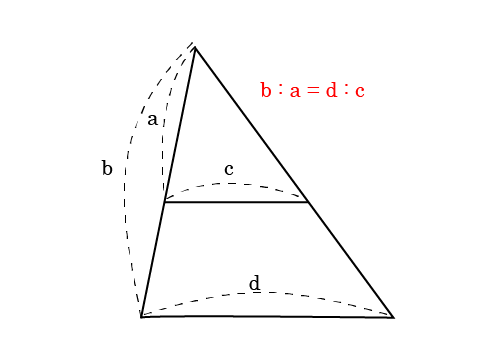
対応する辺の比を考えると辺DH：辺DG＝辺HC：辺GFとなるので、
（x＋6）：x＝8：5
8x＝5（x＋6）
8x＝5x＋30
3x＝30
x＝10
DG＝AEより 求めたい辺AEの長さは10です。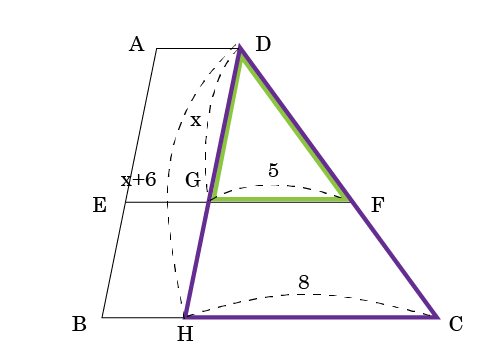
（x＋6）：x＝8：5
8x＝5（x＋6）
8x＝5x＋30
3x＝30
x＝10
DG＝AEより 求めたい辺AEの長さは10です。
完璧！よく出来ました！
解く際のポイントは、Dを通り、辺ABと平行になる補助線を引いて、相似になる三角形を作って考えてみることです。
解く際のポイントは、Dを通り、辺ABと平行になる補助線を引いて、相似になる三角形を作って考えてみることです。
ITTO長野の中学生数学プラン
現在の学習状況や志望校などをお伺いしながらプランはご案内しております。詳しくは各教室まで。例えばこんなプランで
ITTO長野の中学生数学プランのお問い合わせ
LINEで問い合わせ
※下のボタンをクリックして、お友達追加からお名前（フルネーム）とご用件をお送りください。