中学校2年生数学-連立方程式の利用(割合)
単元:連立方程式(割合の文章問題)
問題
ある中学校の生徒数は、昨年度は男女合わせて525人だった。今年度は、男子は4%減り、女子は8%増えて合計525人だった。
今年度の男子と女子の生徒数をそれぞれ求めなさい。

問題の分の中で昨年度の男女の合計生徒数がわかっているので、昨年度の男子と女子の生徒数をそれぞれx人、y人として式を組み立ててみるところから考えてみましょう。

昨年度の生徒数は男女合わせて525人だから、x+y=525 という式で表せると思います。

そうですね!
次は、今年度の生徒数を割合を使って式で表してみましょう。
ポイントは、今年度の男子の生徒数は昨年度より4%減っているので、昨年度の男子の生徒数を100%と考えると、今年度は昨年度の96%になります。 また、割合の関係式で表すと、今年度の生徒数=昨年度の生徒数×割合(百分率)となります。
そうすると、
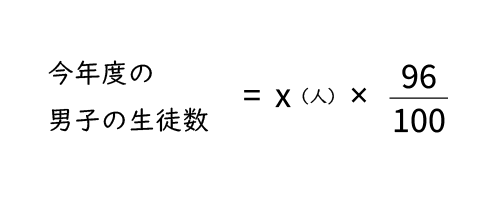
でいいのですか?
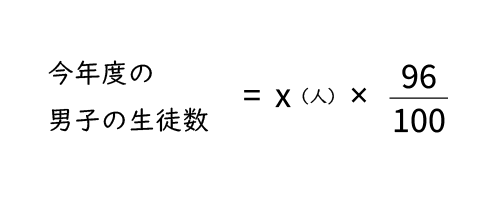
でいいのですか?

その通りです。同様に今年度の女子の生徒数も考えてみましょう。

今年度の女子の生徒数は昨年度より8%増えているので、昨年度の女子の生徒数を100%と考えると、今年度は昨年度の108%になるから、
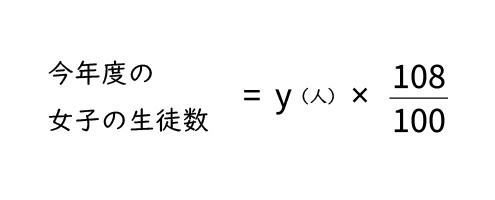 です。
です。
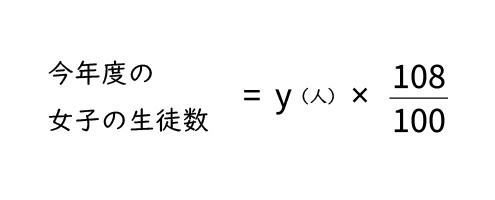 です。
です。

OKです。
それでは、これまでの答えを問題文の通りにまとめると、どのような式になるでしょう。
それでは、これまでの答えを問題文の通りにまとめると、どのような式になるでしょう。

今年度の生徒数も合計525人となるので、
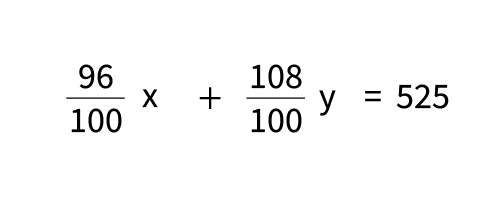 となります。
となります。
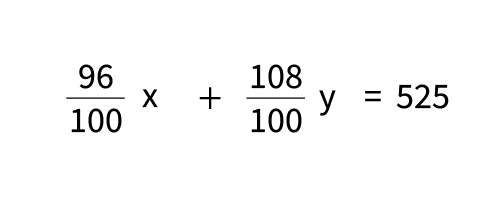 となります。
となります。

素晴らしい!
今年度の生徒数の式と昨年度の生徒数の式を連立方程式として解いてみましょう。
今年度の生徒数の式と昨年度の生徒数の式を連立方程式として解いてみましょう。

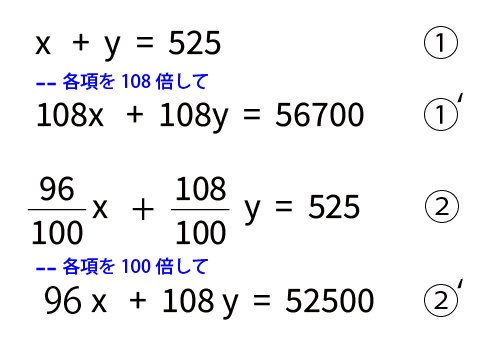

昨年度の女子の生徒数は、175人 となりました。

その調子で、今年度の男子、女子それぞれの生徒数も導いてみましょう。

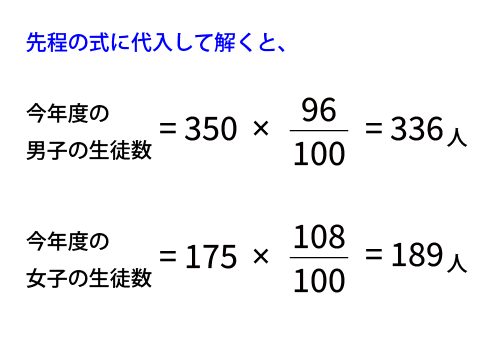 となりました。
となりました。

非常によくできました!
ポイントは、最初にxとyを昨年度の男子生徒数と女子生徒数として考えているので、今年度の生徒数で計算し直すことが大切です。
ポイントは、最初にxとyを昨年度の男子生徒数と女子生徒数として考えているので、今年度の生徒数で計算し直すことが大切です。
ITTO長野の中学生数学プラン
現在の学習状況と志望校などをお伺いしながらプランはご案内しております。詳しくは各教室まで。例えばこんなプランで









