中学校2年生数学-平行四辺形になる条件
単元：平行四辺形になる条件
今日は平行四辺形について学習していくよ。四角形が平行四辺形になる条件についてはもう習ったかな？
はい、先生。
四角形が平行四辺形になる条件は
です。
四角形が平行四辺形になる条件は
です。
その通り！よく覚えましたね。
この①～⑤の条件のどれか１つでも満たしていれば、その四角形は平行四辺形であるといえます。
では次に、四角形 ABCD を使って①～⑤の条件を図形と記号で表してみよう。
この①～⑤の条件のどれか１つでも満たしていれば、その四角形は平行四辺形であるといえます。
では次に、四角形 ABCD を使って①～⑤の条件を図形と記号で表してみよう。
えーと…
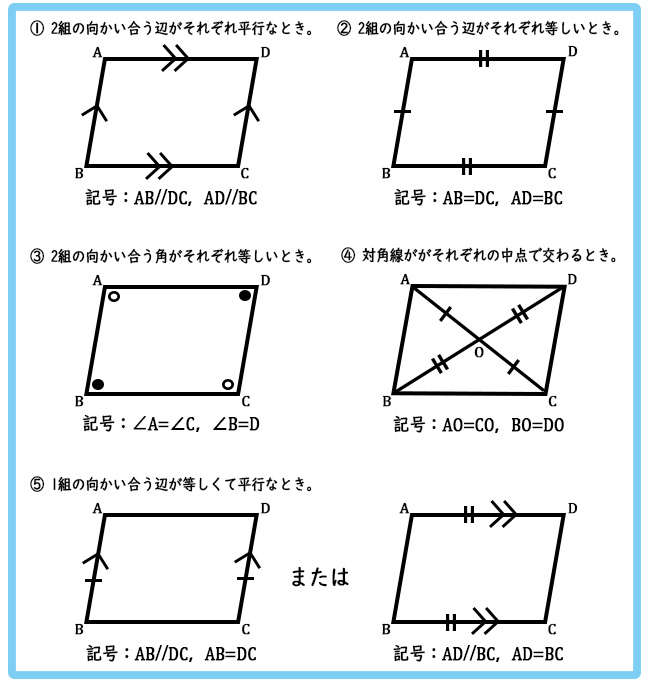
素晴らしい！よく出来ました。平行四辺形になる条件は、言葉だけでなく図形とセットで覚えるのがポイントです。
では、以上のことを踏まえて次の問題を解いてみましょう。
では、以上のことを踏まえて次の問題を解いてみましょう。
問題：次の(1)～(4)のうち、平行四辺形であるといえるものを選びなさい。
(1) AD=5 ㎝、BC＝5 ㎝、AB//CD の四角形 ABCD
(2) 対角線の交点を O とするとき，OA=5 ㎝，OB＝5 ㎝，OC=7 ㎝，OD＝7 ㎝の四角形 ABCD
(3) ∠A＝110°,∠B=70°,∠C=110°,∠D＝70°の四角形 ABCD
(4) AB=8 ㎝，DC＝8 ㎝，∠B＝60°，∠C＝120°の四角形 ABCD
よし。ひとつずつ図形を書いて確認していくぞ。
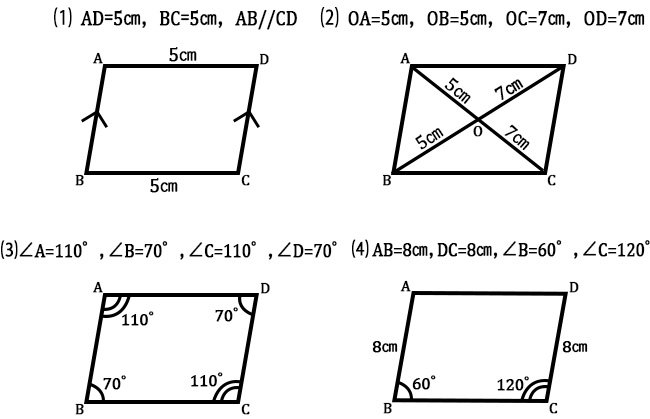
(3)は「2 組の向かい合う角がそれぞれ等しい」から平行四辺形ですね。それ以外は平行四辺形になる条件に当て はまらないと思います。
(3)は「2 組の向かい合う角がそれぞれ等しい」から平行四辺形ですね。それ以外は平行四辺形になる条件に当て はまらないと思います。
正解です!! ……といいたい所なんだけど、(3)以外にもう 1 つあります。実は(4)も平行四辺形であると 言えます。
えっ！そうなんですか!? でも何でだろう……。
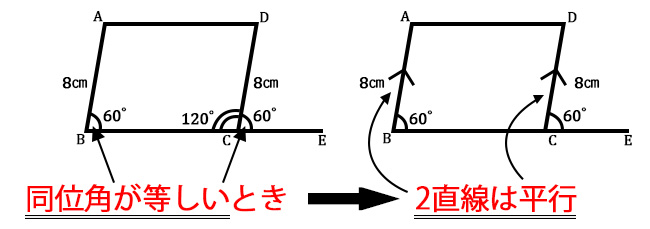
辺 BC を下の図のように少し伸ばしてみましょう。そうすると、∠DCE は 180°－120°で 60°になりま す。
また、∠B と∠DCE は同位角の関係にあります。
すると 2 つとも 60°なので同位角が等しいことから、 AB と DC は平行であるということが分かります。
また、∠B と∠DCE は同位角の関係にあります。
すると 2 つとも 60°なので同位角が等しいことから、 AB と DC は平行であるということが分かります。
そうか！ということは AB＝DC、AB//DC となるから「1組の向かい合う辺が等しくて平行」なので、平行四辺形と言えるのですね。
その通りです! この平行線と角の性質は色々な場面で使うので、 よく覚えておきましょう。
ITTO長野の中学生数学プラン
現在の学習状況と志望校をお伺いしながらプランはご案内しております。詳しくは各教室まで。例えばこんなプランで
ITTO長野の中学生数学プランのお問い合わせ
LINEで問い合わせ
※下のボタンをクリックして、お友達追加からお名前（フルネーム）とご用件をお送りください。