【中２】連立方程式の利用（列車の長さと速さ）
単元：列車の長さと速さの文章問題
今日は連立方程式の文章問題を解いていくよ。
下の問題を見てみよう。
下の問題を見てみよう。
問題
ある列車が、全長1900mのトンネルに入りはじめてから、完全に抜け出るまでに70秒かかった。また、この列車が同じ速さで、全長400mの橋を渡り始めてから完全に渡り終えるまでに20秒かかった。
このときの列車の長さと時速を求めなさい。
列車の問題ですね。
連立方程式の文章問題は、まず問題で求めるものを文字で置くのが基本でしたよね💡。
なので、ここでは列車の長さをxm、速さを時速ykmと置けば良いんでしょうか？
連立方程式の文章問題は、まず問題で求めるものを文字で置くのが基本でしたよね💡。
なので、ここでは列車の長さをxm、速さを時速ykmと置けば良いんでしょうか？
しっかり基本をおさえられていますね！列車の長さはxmでOKです。
ですが速さに関しては、この問題分の時間の単位が秒、長さの単位がmとなっていますので、これに合わせて秒速ymと置いた方が方程式を作りやすいですよ。
問題では時速を聞かれているので、yの値が求められた後に、忘れずに秒速を時速に単位変換しましょう。
ですが速さに関しては、この問題分の時間の単位が秒、長さの単位がmとなっていますので、これに合わせて秒速ymと置いた方が方程式を作りやすいですよ。
問題では時速を聞かれているので、yの値が求められた後に、忘れずに秒速を時速に単位変換しましょう。
わかりました。気をつけます。
列車の長さをxm、速さを秒速ymと置いて考えます。
でも、どうやって方程式を作ったら良いんでしょうか？
列車の長さをxm、速さを秒速ymと置いて考えます。
でも、どうやって方程式を作ったら良いんでしょうか？
文章だけだとイメージしづらいですよね。
下の図は、列車がトンネルを入り始めてから出終わるまでを図にしたものです。
これを見ると、 「トンネルの長さ＋列車の長さ」と「列車が進んだ道のり」が同じ長さであることが分かりますよね。
トンネルの長さは1900m、列車の長さはxm、列車が進んだ道のりは、「列車の速さ×進んだ時間」より、y×70＝70yとなるので、1900＋x＝70yという方程式を作ることが出来ます。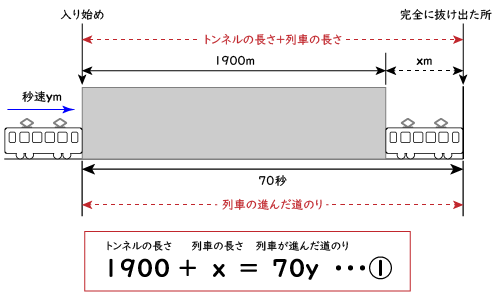
下の図は、列車がトンネルを入り始めてから出終わるまでを図にしたものです。
これを見ると、 「トンネルの長さ＋列車の長さ」と「列車が進んだ道のり」が同じ長さであることが分かりますよね。
トンネルの長さは1900m、列車の長さはxm、列車が進んだ道のりは、「列車の速さ×進んだ時間」より、y×70＝70yとなるので、1900＋x＝70yという方程式を作ることが出来ます。
そうか！そうすると橋の方も同じ考え方で出来そうですね。
下のように「橋の長さ+列車の長さ＝列車が進んだ道のり」となるので、方程式は400+x=20yとなります。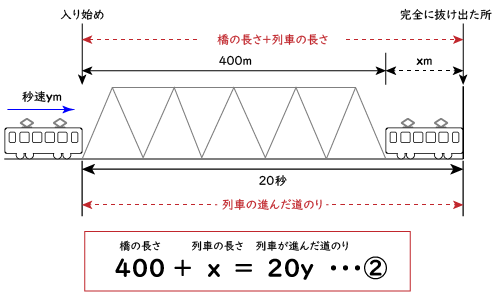
下のように「橋の長さ+列車の長さ＝列車が進んだ道のり」となるので、方程式は400+x=20yとなります。
その通りです。そうしたら①、②を連立方程式として解きます。
計算すると、(x、y)＝(200，30)となりますので、列車の長さは200m，速さは秒速30ｍとなります。 ただし、問題では時速を聞いていますので、秒速30m×3600＝時速108000m＝時速108kmとなり、速さは時速108㎞となります。
ちなみに速さの単位変換の方法は下のようになります。中学校でも時々使うことがあるので必ず覚えておきましょう。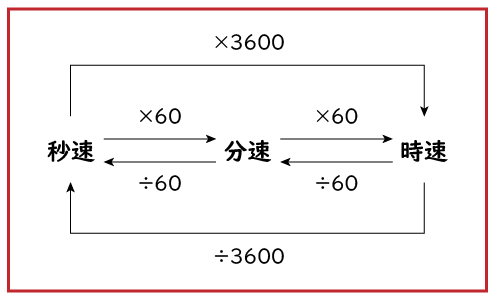
計算すると、(x、y)＝(200，30)となりますので、列車の長さは200m，速さは秒速30ｍとなります。 ただし、問題では時速を聞いていますので、秒速30m×3600＝時速108000m＝時速108kmとなり、速さは時速108㎞となります。
ちなみに速さの単位変換の方法は下のようになります。中学校でも時々使うことがあるので必ず覚えておきましょう。
はい！わかりました！
ITTO長野の中学生数学プラン
現在の学習状況と志望校などをお伺いしながらプランはご案内しております。詳しくは各教室まで。例えばこんなプランで
ITTO長野の中学生数学プランのお問い合わせ
LINEで問い合わせ
※下のボタンをクリックして、お友達追加からお名前（フルネーム）とご用件をお送りください。