中学校3年生数学-有理数と無理数
単元：有理数と無理数の解説とアドバイス
今日は「有理数」と「無理数」について学習していくよ。
これまでの数学では整数や分数、小数、平方根などのいろいろな数について学習してきたけど、
これらの数は大きく「有理数」と「無理数」の2つに分けることができます。
「有理数」と「無理数」ですか？
何だか難しそうですね。その2つは何なんですか？
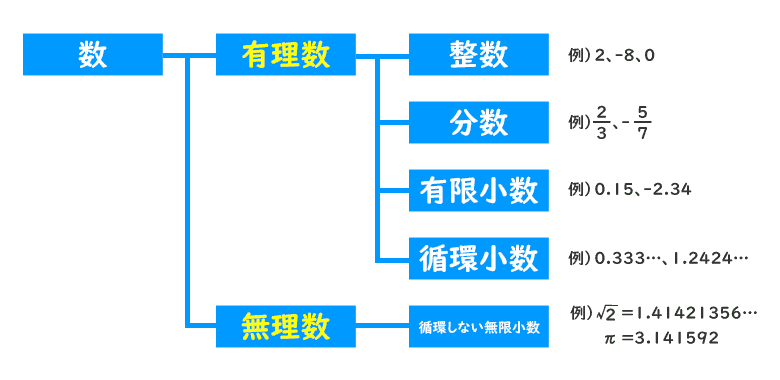
整数、分数が有理数なのは分かるのですが、上の図の「有限小数」、「循環小数」、「循環しない無限小数」って何ですか？
あと、循環しない無理少数だけが何で無理数なんですか？
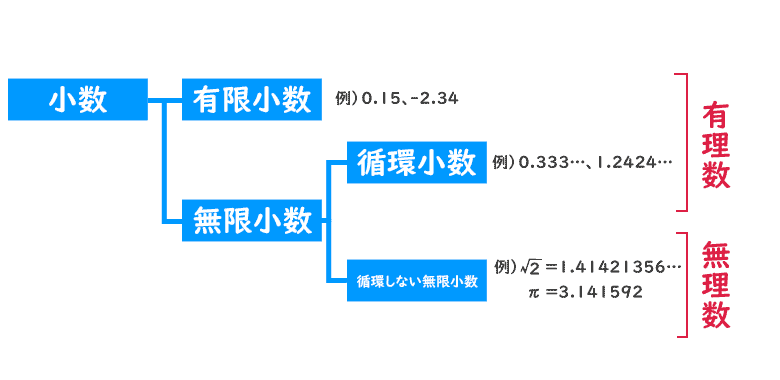
下の図を見てください。
少数はまず「有限小数」と「無限小数」に分けられます。
「有限小数」は0.15や-2.4のように終わりのある小数で、無限小数は、1.3245…や、0.33333…のように無限に続く小数です。
さらに、「無限小数」は、「循環小数」と「循環しない無限小数」に分けられます。
「循環小数」は、0.353535…や1.204204204…のように同じ数字が繰り返し続く無限小数で、1.238974216…のような循環小数を「循環しない無限小数」といいます。
なるほど!!小数にも色々種類があるんですね。
そうすると、「有限小数」と「循環小数」は「有理数」となっているので、どちらも分数で表せるということですか？
その通りです!
その一方で、「循環しない無限小数」だけが分数で表すことができません。
そうか！だから無理数に含まれるのは循環しない無理小数だけなんですね。
そうすると、√2＝1.41421356…や、π＝3.141592…も循環しない無限小数だから無理数なんですね。
その通りです。逆を言えば循環しない無限小数以外の数はすべて有理数となります。
ではこれまで内容を踏まえて次の問題を解いてみよう！
循環しない無限小数になるのは、√5＝2.2360679…と2π＝2×3.1415…だから、アとエは無理数です。
よってそれ以外の、イ・ウ・オ・カ・キは有理数になります。
素晴らしい！正解です！よく理解できています。
ITTO長野の中学生数学プラン
現在の学習状況や志望校などをお伺いしながらプランはご案内しております。詳しくは各教室まで。例えばこんなプランで
ITTO長野の中学生数学プランのお問い合わせ
LINEで問い合わせ
※下のボタンをクリックして、お友達追加からお名前（フルネーム）とご用件をお送りください。