中学校2年生数学-箱ひげ図（四分位数とグラフ）
箱ひげ図の計算の解き方
問題
次のデータは1年1組男子13人の数学のテストである。これについて次の問いに答えなさい。
62 37 72 35 69 24 83 91 33 96 44 81 53 （単位：点）
（1）範囲を求めなさい。
（2）第1四分位数を求めなさい。
（3）第2四分位数を求めなさい。
（4）第3四分位数を求めなさい。
（5）四分位範囲を求めなさい。
（6）下の図に、箱ひげ図を書きなさい。
こうしたデータの問題は、まず、データを小さい順に並べ替えることが重要です。
小さい順に並べ替えてみましょう。
小さい順に並べ替えてみましょう。
小さい順ですね。
24 33 35 37 44 53 62 69 72 81 83 91 96
これでよいでしょうか？
24 33 35 37 44 53 62 69 72 81 83 91 96
これでよいでしょうか？
OKです！
(1)範囲とは最大値と最小値の差になります。
範囲＝最大値ー最小値
並べ替えたデータを見て解いてみましょう。
小さい順に並べ替えてみましょう。
(1)範囲とは最大値と最小値の差になります。
範囲＝最大値ー最小値
並べ替えたデータを見て解いてみましょう。
小さい順に並べ替えてみましょう。
最小値＝24
最大値＝96だから
範囲＝96-24＝72
これでいいですか？
最大値＝96だから
範囲＝96-24＝72
これでいいですか？
正解です！
次に四分位数について考えてみましょう。
データを小さい順に並べ、前半部分の中央値を第1四分位数、データ全体の中央値を第2四部位数、後半部分の中央値を第3四分位数と言います。
また、四分位範囲は、第1四分位数と第3四分位数の差になります。
例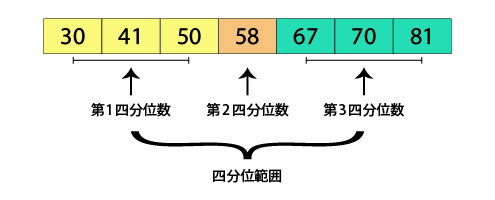
この場合は、第1四分位数＝41
第2四分位数＝58
第3四分位数＝70
四分位範囲は、70-41＝29となります。
次に四分位数について考えてみましょう。
データを小さい順に並べ、前半部分の中央値を第1四分位数、データ全体の中央値を第2四部位数、後半部分の中央値を第3四分位数と言います。
また、四分位範囲は、第1四分位数と第3四分位数の差になります。
例
この場合は、第1四分位数＝41第2四分位数＝58
第3四分位数＝70
四分位範囲は、70-41＝29となります。
わかりました。同じように考えてみます。
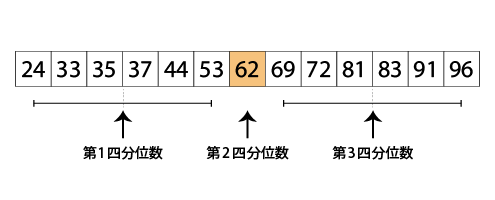あれ？前半部分のデータが6個と偶数だから、真ん中の値が決められません。
この場合は、どのように考えたらいいですか？
あれ？前半部分のデータが6個と偶数だから、真ん中の値が決められません。この場合は、どのように考えたらいいですか？
その場合は35点と37点の中央値を計算して出す必要があります。
そうすると、（35+37）÷2＝36点 でいいですか？
正解です。
第1四分位数は36点です。第2四分位数と第3四分位数も考えてみましょう。
第1四分位数は36点です。第2四分位数と第3四分位数も考えてみましょう。
わかりました。
第2四分位数は、全体の中央値になるので、62点ですね。
第3四分位数は、（81＋83）÷2＝82点 ですね。
第2四分位数は、全体の中央値になるので、62点ですね。
第3四分位数は、（81＋83）÷2＝82点 ですね。
その通りです。
四分位範囲は、第1四分位数36点と第3四分位数82点の差だから
四分位数範囲＝82点ー36点＝46点 ですね。
四分位数範囲＝82点ー36点＝46点 ですね。
正解です。
最後に箱ひげ図を書いてみましょう。
箱ひげ図は、下記のように定義されています。参考にして作ってみましょう。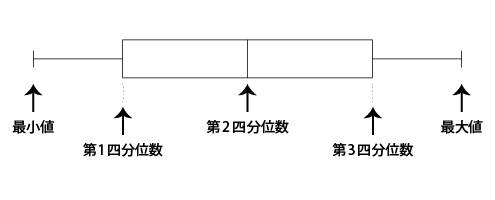
最後に箱ひげ図を書いてみましょう。
箱ひげ図は、下記のように定義されています。参考にして作ってみましょう。
これで合ってますか？
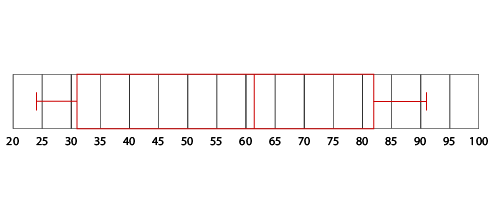
よくできました！
参考までに箱ひげ図の見方について解説します。
箱の区間は、全体の２５％の割合に相当します。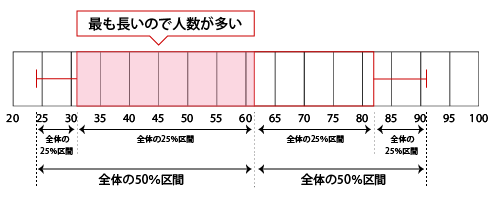
箱ひげ図が便利な点は、ぱっと見て、どの区間に人数が多いのかが一目でわかることです。
例えば、今回の問題で書いた箱ひげ図は、第1四分位数から第2四分位数の区間が最も長いので、全体で最も人数が多いことがわかります。
参考までに箱ひげ図の見方について解説します。
箱の区間は、全体の２５％の割合に相当します。
箱ひげ図が便利な点は、ぱっと見て、どの区間に人数が多いのかが一目でわかることです。例えば、今回の問題で書いた箱ひげ図は、第1四分位数から第2四分位数の区間が最も長いので、全体で最も人数が多いことがわかります。
ITTO長野の中学生数学プラン
現在の学習状況と志望校をお伺いしながらプランはご案内しております。詳しくは各教室まで。例えばこんなプランで
ITTO長野の中学生数学プランのお問い合わせ
LINEで問い合わせ
※下のボタンをクリックして、お友達追加からお名前（フルネーム）とご用件をお送りください。