中学校2年生数学-三角形の合同（証明問題）
単元：三角形の合同証明の問題
今日は合同の証明をやっていこう。早速、問題です。
図1のように、正方形ABCDと正方形CEFGがある。
この時、∠CBG＝∠CDEであることを証明せよ。
図2の中の等しい辺や角に同じ印をつけ△BCG≡△DCEとなることを利用して解きなさい。
図1のように、正方形ABCDと正方形CEFGがある。
この時、∠CBG＝∠CDEであることを証明せよ。
図2の中の等しい辺や角に同じ印をつけ△BCG≡△DCEとなることを利用して解きなさい。
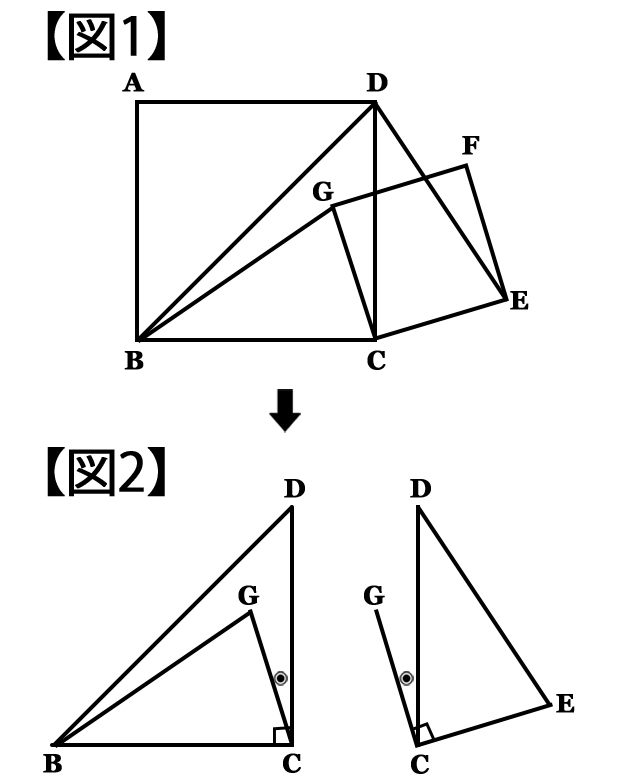
まず、図2で等しい辺と角度を探してみると
正方形は辺が等しいから、
正方形は辺が等しいから、
BC＝DC・・・①、
GC＝EC・・・②
は見えました。
いいですね！
あとは、角度が同じところがあるけどわかるかな？
あとは、角度が同じところがあるけどわかるかな？
図2で、正方形の90°が両方の図形にあってその間の角が共通角だから
∠BCG＝ 90°－∠GCD
∠DCE＝ 90°－∠GCD より、
∠BCG＝∠DCE・・・③
そうすると、①、②、③より△BCGと△DCEが合同条件を使って証明できそうです。
とても良い推察です！
では、合同条件を手順にそって記載してみよう。
では、合同条件を手順にそって記載してみよう。
やってみます。
①、②、③より、2組の辺とその間の角がそれぞれ等しいので、
△BCG≡△DCE
合同な図形は対応する角がそれぞれ等しいので
∠CBG＝∠CDE が言える。
どうですか？
正解です！
証明は合同手順を、番号を使ってしっかり明記することが大切です。
合同条件は、必ず書くようにしましょう。
証明は合同手順を、番号を使ってしっかり明記することが大切です。
合同条件は、必ず書くようにしましょう。
ITTO長野の中学生数学プラン
現在の学習状況と志望校をお伺いしながらプランはご案内しております。詳しくは各教室まで。例えばこんなプランで
ITTOの中学生数学プランのお問い合わせ
LINEで問い合わせ
※下のボタンをクリックして、お友達追加からお名前（フルネーム）とご用件をお送りください。