中学校1年生数学-おうぎ形（影のついた部分の面積）
単元：複雑な面積の求め方
下の図の影になっている部分の面積を求めてください。
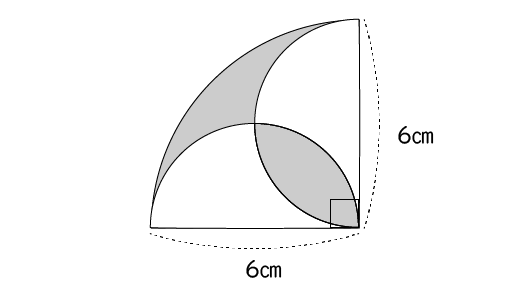
扇形の半分の図形からうまく残りの白部分を引いた式ができれば解けそうですね。
Goodです。さてどのように引いたらよいでしょうか。
ヒントは、図の部分に線を書き入れると驚くほど簡単に求めることができます。
ヒントは、図の部分に線を書き入れると驚くほど簡単に求めることができます。
2本の線を入れてみました。
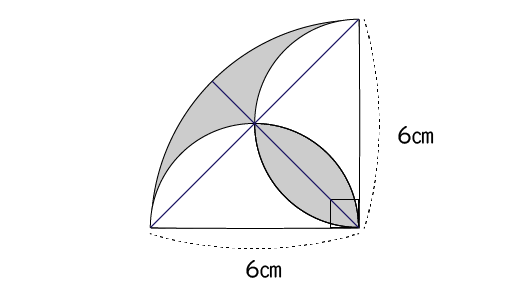
中央の半月の部分がどこかに重なるような…
中央の半月の部分がどこかに重なるような…
あ！そうか！中央の半月の部分は左上の部分と同じ図形ができているから移動したら残りは大きな半月の部分に切り替えができそうです。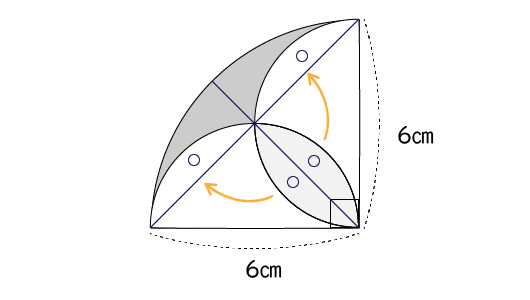
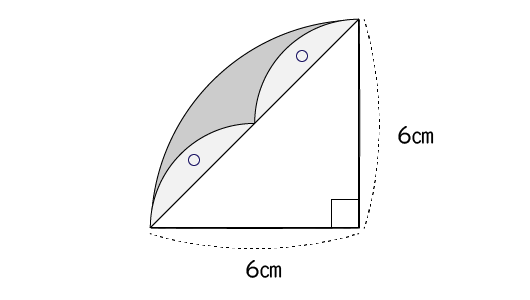
お見事！
次に式を考えてみましょう。
次に式を考えてみましょう。
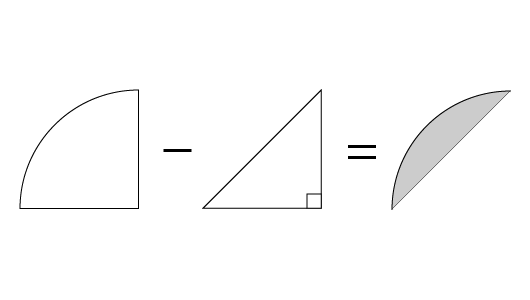
だから、円の4分の1の扇形 － 直角三角形 ＝ 影の部分の面積 ？
円の面積は、π×半径×半径だから、
（1／4 × π × 6 × 6）ー （1／2 × 6 × 6）＝ 9π-18㎠
（1／4 × π × 6 × 6）ー （1／2 × 6 × 6）＝ 9π-18㎠
正解！完璧です！
アドバイスとしては、内側に線を引いて同じ図形が見えたら、その図形を分割して移動させてみることです。
期末テストに良く出る問題なので充分研究しておきましょう。
アドバイスとしては、内側に線を引いて同じ図形が見えたら、その図形を分割して移動させてみることです。
期末テストに良く出る問題なので充分研究しておきましょう。
長野県長野市の中学生数学特訓プラン
各自の実力と志望高、目的に合わせプランはカスタマイズしてご提案しております。詳しくは各教室まで。
基礎力養成特訓プラン
| 推奨学年 | 中学1年～中学3年生 |
| 内容 | 計算の基礎養成演習 |
| 時間割 | 50分授業×週1回 |
| 授業回数 | 月間4回 |
| 授業料 | 中学1年生：9,130円(税込) |
| 中学2年生：9,570円(税込) | |
| 中学3年生：9,790円(税込) |
発展力養成特訓
| 推奨学年 | 中学1年～中学3年生 |
| 内容 | 文字式・方程式・関数・証明等の文章題読解演習 |
| 時間割 | 50分授業×週1回 |
| 授業回数 | 月間4回 |
| 授業料 | 中学1年生：9,130円(税込) |
| 中学2年生：9,570円(税込) | |
| 中学3年生：9,790円(税込) |
各種理科特訓プランは以下からお問い合わせ下さい。
LINEで問い合わせ
※下のボタンをクリックして、お友達追加からお名前（フルネーム）とご用件をお送りください。