中学校3年生数学-平方根の性質
単元:平方根の性質と応用問題

今日は平方根について学習していくよ。
まず、平方根とは何か知っているかな?

それなら習いました!
2乗して𝑎になる数を、𝑎の平方根というんですよね?

その通りです!
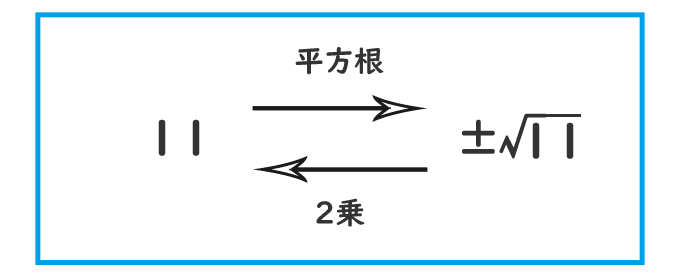
では、11の平方根はどうなるでしょうか?

11の平方根は、25の平方根のように整数では表せないから、√(ルート)という記号を使って、
√11と−√11、まとめて±√11と書きます。

素晴らしい説明です!
では、ここまでの内容をまとめてみましょう。


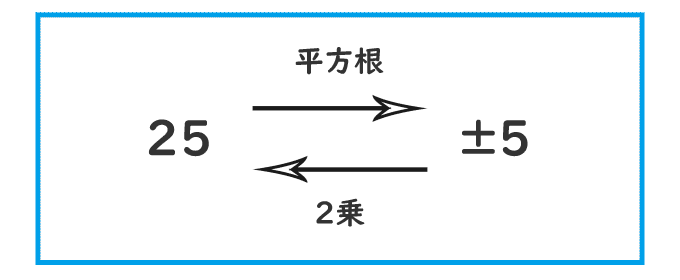
では、次に25の平方根についてもう少し考えてみましょう。
25の平方根は5と-5ですが、√を使って表すと√25、ー√25とも表すこともできますね。
そうすると、√25は25の平方根のうち正の数なので、√25=5、ー√25は負の数なのでー√25=-5となります。
そう考えてると√25=√52=5のように、√の中が2乗の形で表せるものは必ず整数となります。


そうです!
ただし、√(-5)2ような時は、√(-5)2=ー5とはならず、√(-5)2=√25=5となるので注意しましょう。


では次に,この性質を使って次の応用問題を解いてみましょう。
問題:√84𝑛が整数となるような最小の自然数𝑛の値を求めよ。またその時、√84𝑛はどのような整数となるか。

√84𝑛が整数となるためには、84𝑛=𝑎2の形になるような𝑛の値を考えればよさそうですね。
うーん、1から順番にnに代入して考えていけばよいのかな。

それでは時間がかかってしまうので違う方法を考えてみましょう。
まずは84を素因数分解します。そうすると 84𝑛=2×2×3×7×𝑛となります。ここで、𝑛=3×7を代入してみましょう。
すると、次のような式変形ができます。
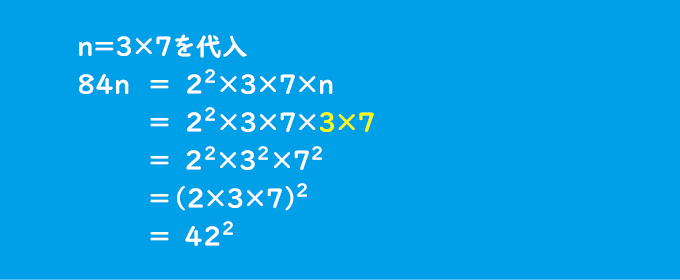

なるほど!
84を素因数分解した後、全ての因数が2乗となるような𝑛の値を考えれば良いのですね!
そうすると、𝑛=3×7=21のとき、
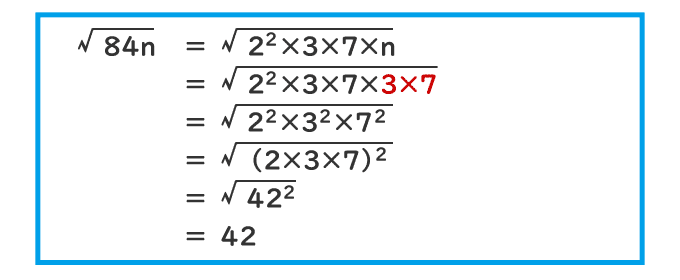
よって
𝑛=21のとき、√84𝑛=42となります。

正解です!!
この他にも、平方根の性質に関する問題やそれを利用する問題はたくさんあるので、積極的に取り組んでみましょう。
長野県長野市の中学生数学特訓プラン
各自の実力と志望高、目的に合わせプランはカスタマイズしてご提案しております。詳しくは各教室まで。
基礎力養成特訓プラン
| 推奨学年 | 中学1年~中学3年生 |
| 内容 | 計算の基礎養成演習 |
| 時間割 | 50分授業×週1回 |
| 授業回数 | 月間4回 |
| 授業料 | 中学1年生:9,130円(税込) |
| 中学2年生:9,570円(税込) | |
| 中学3年生:9,790円(税込) |
発展力養成特訓
| 推奨学年 | 中学1年~中学3年生 |
| 内容 | 文字式・方程式・関数・証明等の文章題読解演習 |
| 時間割 | 50分授業×週1回 |
| 授業回数 | 月間4回 |
| 授業料 | 中学1年生:9,130円(税込) |
| 中学2年生:9,570円(税込) | |
| 中学3年生:9,790円(税込) |








