【中1】数の大小(正負の数)
単元:数の大小問題の解き方

今日は数の大小について学習していくよ。さっそくですが問題です。-3と+2は,どちらの方が大きいでしょう?

そんなの簡単だよ。プラスの数の方が大きいから、+2です。

正解です!ちなみに不等号を使って表すと
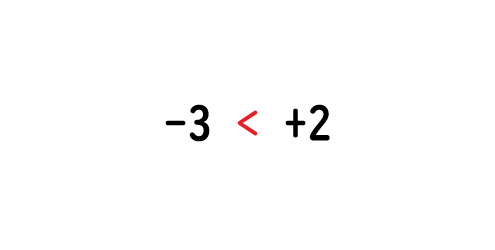 となります。不等号は、数の大きい方に向かって開くように書きましょう。
となります。不等号は、数の大きい方に向かって開くように書きましょう。
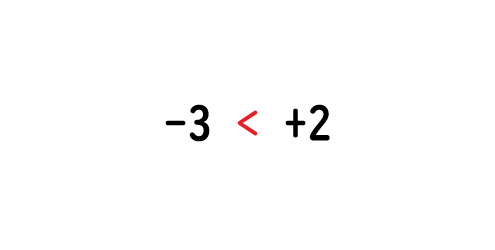 となります。不等号は、数の大きい方に向かって開くように書きましょう。
となります。不等号は、数の大きい方に向かって開くように書きましょう。
それでは,次の問題です。-2と-5はどちらの方が大きい数でしょうか。その大小関係を不等号で表してみましょう。

うーん。今度はどちらも負の数ですね。
-5の方が数字の部分が大きいから、-5だと思います。
よって不等号を使って表すと、-2<-5となります。
-5の方が数字の部分が大きいから、-5だと思います。
よって不等号を使って表すと、-2<-5となります。

残念!
大きい方の数は-2です。よって大小関係を不等号で表すと、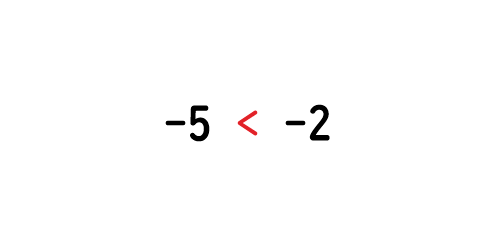 となります。このことは、数直線を使って考えるとわかりやすいですよ。
となります。このことは、数直線を使って考えるとわかりやすいですよ。
数の大きさは、数直線上では右にある数ほど大きく,左にある数ほど小さくなります。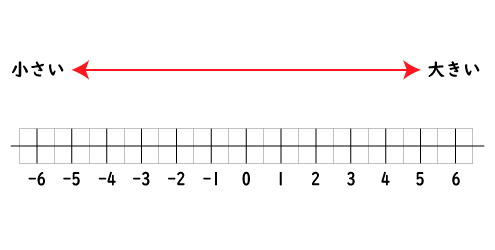
大きい方の数は-2です。よって大小関係を不等号で表すと、
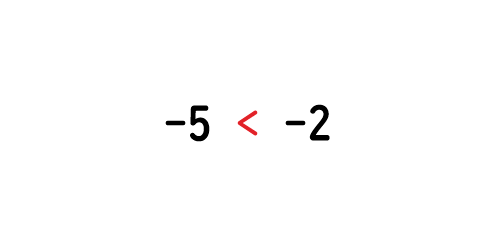 となります。このことは、数直線を使って考えるとわかりやすいですよ。
となります。このことは、数直線を使って考えるとわかりやすいですよ。
数の大きさは、数直線上では右にある数ほど大きく,左にある数ほど小さくなります。


なるほど。つまり負の数は、,数字の部分が大きいほど数自体は小さくなるんですね!

その通りです!では次に,-2,4,-8の大小関係を不等号で表してみましょう。

-2と-8はどちらも4より小さいから、
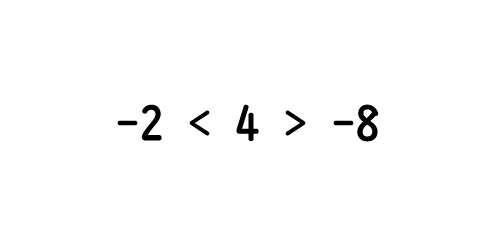 です!
です!
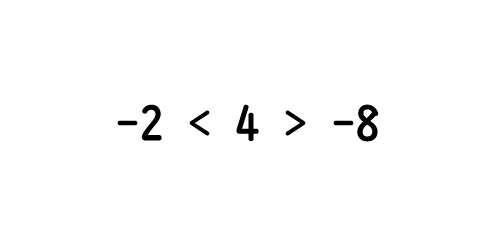 です!
です!
なるほど。でもその式を見ると,-2と-8の大小関係が分からないですね。
数が3つ以上の場合は,まず数の小さい順に並べてから不等号を書いてみて下さい。
数が3つ以上の場合は,まず数の小さい順に並べてから不等号を書いてみて下さい。

わかりました!3つの数を小さい順に並べると-8,-2,4だから,これに不等号を書き加えると
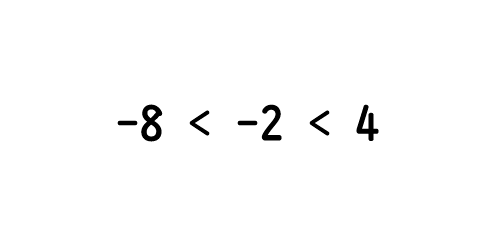 になります!
になります!
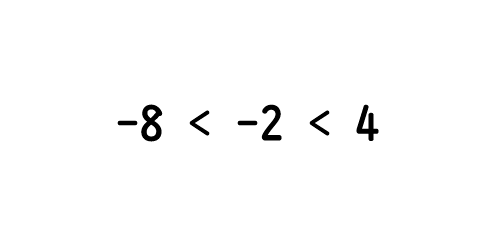 になります!
になります!
正解です!数が3つ以上の時は、必ず不等号の向きをそろえるようにしましょう。
では最後の問題です。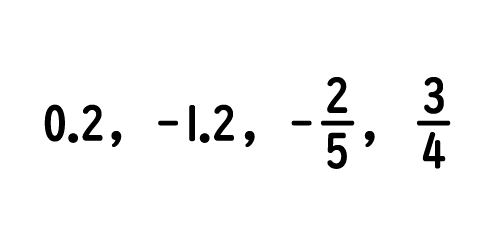 の大小関係を不等号で表すとどうなるでしょうか。
の大小関係を不等号で表すとどうなるでしょうか。
では最後の問題です。
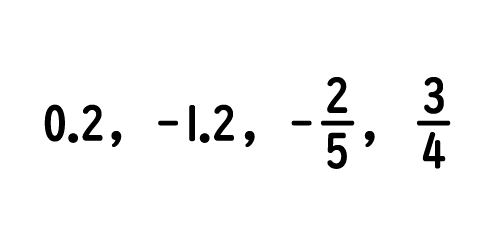 の大小関係を不等号で表すとどうなるでしょうか。
の大小関係を不等号で表すとどうなるでしょうか。
うーん,このままだと大小関係が分かりづらいので、分数を小数で表してみます。
分数を小数にするには分子÷分母の計算をすればよいから、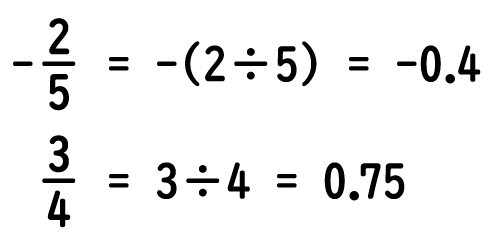 となります。
となります。
そして4つの数を小さい順にならべて不等号を使って表すと,-1.2<-0.4<0.2<0.75となるので。最後に-0.4と0.75を分数の形に戻して,答えは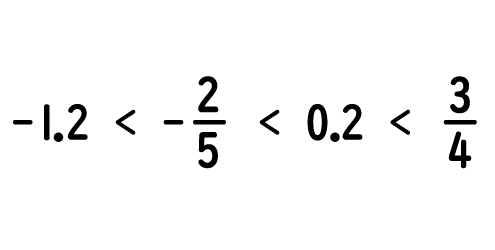 になります!
になります!
分数を小数にするには分子÷分母の計算をすればよいから、
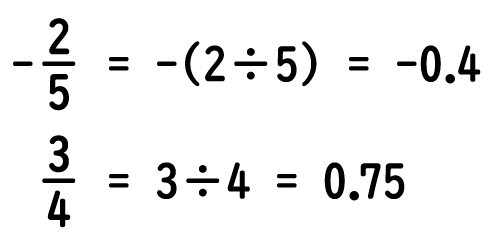 となります。
となります。そして4つの数を小さい順にならべて不等号を使って表すと,-1.2<-0.4<0.2<0.75となるので。最後に-0.4と0.75を分数の形に戻して,答えは
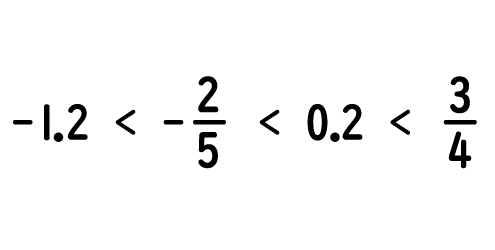 になります!
になります!
大正解です!よくできました!
これで数の大小はバッチリですね。
これで数の大小はバッチリですね。
ITTO長野の中学生数学プラン
現在の学習状況と志望校をお伺いしながら、プランをご案内しております。詳しくは各教室まで。例えばこんなプランで









