令和3年長野県公立高校入試問題 数学問2 Ⅱ(1)解説
春さんの学校では、生徒会企画の運動会の準備を進めている。
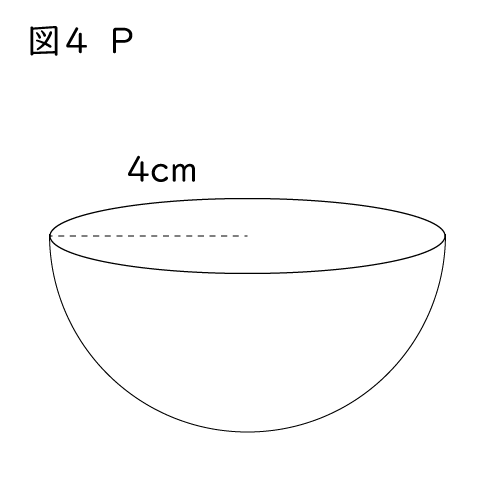
(1)水を運ぶ競技で使うために、図4のような、水を入れる容器PとQを準備した。Pは半径4cmの半球、Qは底面の半径が4cm、高さが8cmの円錐である。ただし、容器の厚さは考えないものとする。
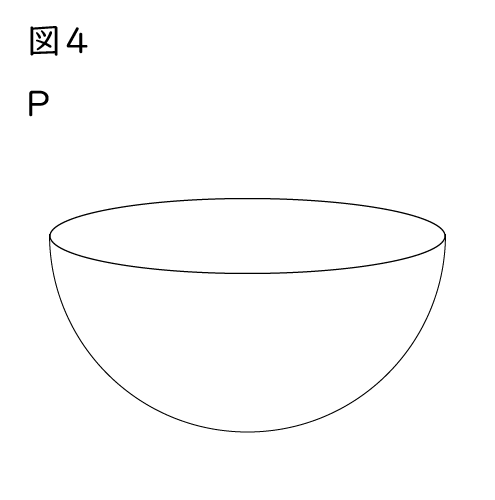
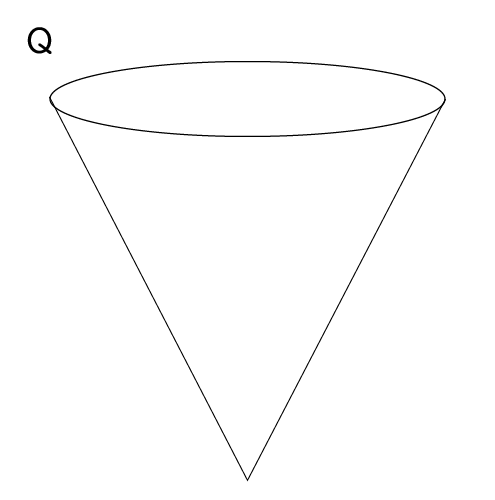
① Qに水をいっぱいに入れたときの水の体積Vを求める次の式について、【あ】に当てはまる数を書きなさい。
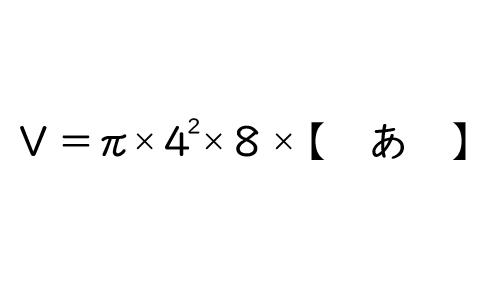
② PとQそれぞれに水をいっぱいに入れたときの水の体積を比較したとき、どのようなことはいえるか、最も適切なものを次のア~ウから1つ選び記号を書きなさい。また、そのようにいえる理由を説明しなさい。
ア PとQの水の体積は等しい。
イ Pの水の体積の方が大きい。
ウ Pの水の体積の方が小さい。
① Qの円錐の体積は以下の公式で求めることができます。

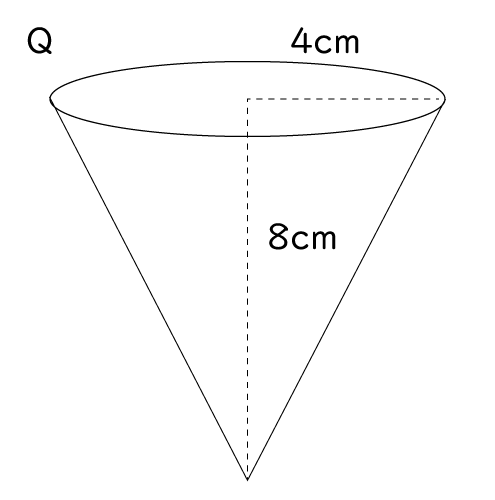
上の公式に、問題文より底面積(円の面積=4×4×π)と高さ8cmを代入すると、円錐の体積=42π×8×1/3で求められ、【あ】に当てはまるのは、1/3となります。
② Pの半球(球の半分)の体積は、以下の公式を半分(1/2)にして求めることができます。
上の公式に、問題文より半径4cmを代入すると、半球の体積=4/3π×43×1/2で求められ、=128/3πとなります。
①より、Qの体積は、=42π×8×1/3で求められるので、=128/3πとなります。
よって、PとQはいずれも同じ体積128/3πcm3となり、答えは、ア PとQの水の体積は等しい。となります。
またその理由は、上記の計算式をまとめて、

PとQの体積がP:Q=1:1となっているから、PとQの水の体積は等しい。
POINT!
理由の説明書きのは、採点のポイントとして、”PとQがそれぞれ体積が同じになる計算式”と”PとQの体積比が1:1になっていること”が書かれていればOKです。
また、球の表面積や立体の表面積の求め方も一緒に一度確認しておくとさらによいですね。
長野県長野市の数学特訓プラン
基礎力養成特訓プラン
| 推奨学年 | 中学1年~中学3年生 |
| 内容 | 計算の基礎養成演習 |
| 時間割 | 50分授業×週1回 |
| 授業回数 | 月間4回 |
| 授業料 | 中学1年生:8,300円 |
| 中学2年生:8,700円 | |
| 中学3年生:8,900円 |
発展力養成特訓
| 推奨学年 | 中学1年~中学3年生 |
| 内容 | 文字式・方程式・関数・証明等の文章題読解演習 |
| 時間割 | 50分授業×週1回 |
| 授業回数 | 月間4回 |
| 授業料 | 中学1年生:8,300円 |
| 中学2年生:8,700円 | |
| 中学3年生:8,900円 |









