2025【川中島校】2学期期末テストの解き方:中2 数学
今回は…
一次関数の問題をピックアップするよ
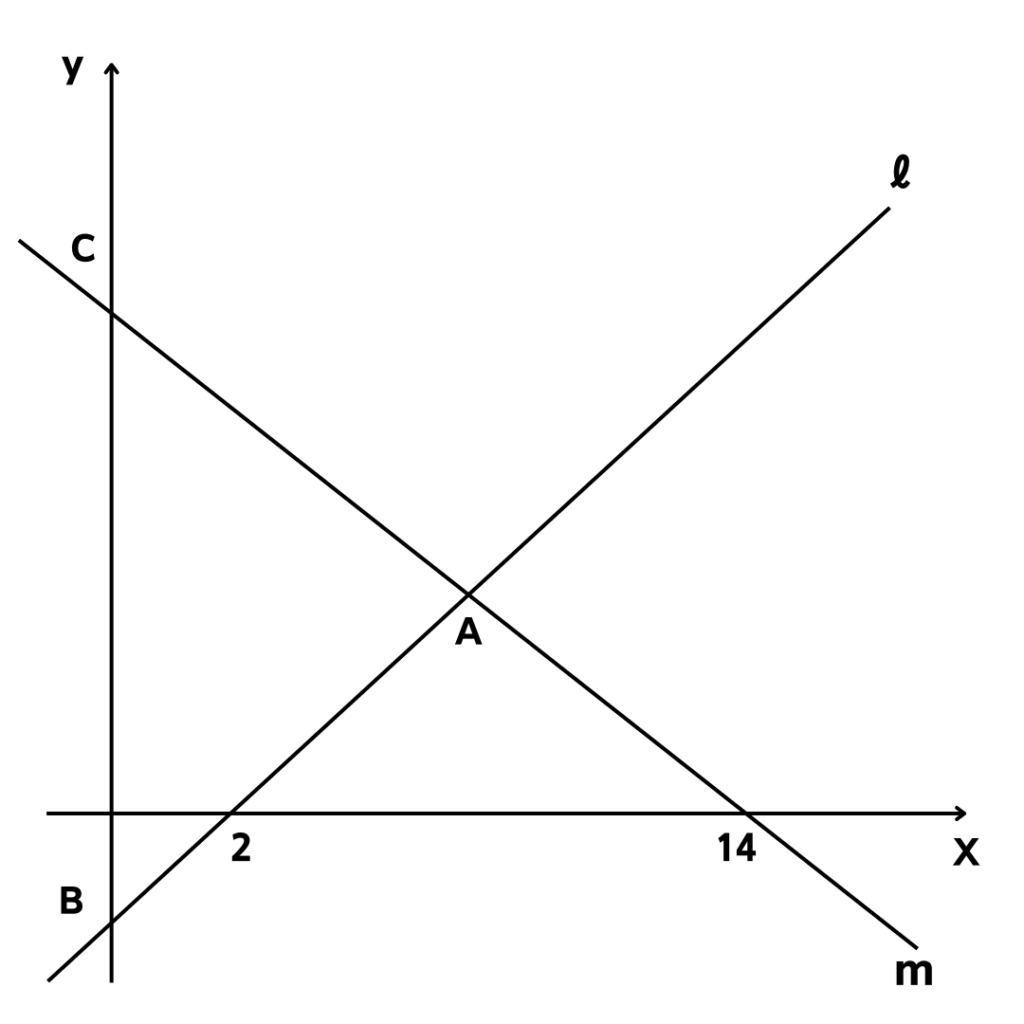
\(直線\:ℓ\:と直線\:m\:が点\:A\:で交わっている。\)
\(直線\:ℓ\:の傾きは1、直線\:m\:の傾きは-1である。\)
\(また、直線\:ℓ\:と\:y\:軸との交点をB、\)
\(直線\:m\:と\:y\:軸との交点を\:C\:とし、\)
\(直線\:ℓ\:と直線\:m\:の\:x\:軸との交点は\)
\( それぞれ(2,0)、(14,0)とする。\)
\(このとき、次の問いに答えなさい。\)

は-い🙋♀️
では始めていきましょ。
一次関数のグラフの問題だね💡
一次関数のポイントは…
☝️式が出てれば通る点の座標が出せる
✌️通る点の座標が出てれば式が出せる
基本この繰り返しだね。
この問題は点Aの座標を求めなさい。ってことだよね。
交点の座標は交わる2直線の式を連立方程式で解くと出せるから。
だから、とりあえずℓとmの式を出さないとだね。
まずは一次関数の式がどう表せるかだね。
うらのさん、お願いします🙏

おまかせください✍️
一次関数の式は…
\(\bbox[pink,4px]{\:y=ax+b}\)で、\(\bbox[pink,4px]{\:a\:は傾き}で、\bbox[pink,4px]{\:b\:が切片}だよね。\)
こうだったような…。
つきは先生いいですか?

OK👌
いい感じで知識が入ってるね✨
では、
\(まずは直線\:ℓ\:の式から出してみよう❗\)\(\large{直線\:ℓ\:の傾きは1で、}\)
\(\large{x\:軸との交点は\:(2,0)\:}\)
\(って、問題に書いてある。\)
さあ、うらのさん、やってみよう✍️

ほーい🤚
\(直線\:ℓ\:は…\)\[\:y=ax+b\]
\(傾きが、1だから、aは1ってことなので\)
\[y=x+b\]
ここに、座標が(2,0)なので…
\(x\:に2、y\:に0を代入して\)
\[0=2+b\]
\(見にくいから、左辺と右辺を入れ替えて…\)
\[2+b=0\] \[b=-2\]
これを代入して
\[\bbox[orange,4px]{y=x-2}\]
つきは先生できました❗

すばらしい👏
ではでは、
\(直線\:m\:の式もお願いします❗\)ちなみに
\(直線\:m\:の傾きは-1で、\)
\(x\:軸との交点は\:(14,0)\:って\)
\(問題に書いてあるよ。\)

いけるよ😆
\(直線\:m\:は…\)\[\:y=ax+b\]
\(傾きが、-1だから、aは-1だから\)
\[y=-x+b\]
座標が(14,0)なので…
\(x\:に14、y\:に0を代入して\)
\[0=-14+b\]
\(見にくいから、左辺と右辺を入れ替えて…\)
\[-14+b=0\] \[b=14\]
これを代入して
\[\bbox[lightgreen,4px]{y=-x+14}\]
つきは先生、OKでしょ❓

めっちゃいいね🎉
これで2つの直線の式がでました。
これで交点の座標が求められるね👍
2つの直線が同じ点を通らないといけない。
たから、両方の式で成り立つものが欲しい。
そこで、連立方程式の解を求めるってことだね。
うらのさん、あとはおまかせしやす😆

かしこまりました🙌
\[直線\:ℓ\:は\:y=x-2\] \[直線\:m\:は\:y=-x+14\]これを連立してっと
\begin{eqnarray} \left\{ \begin{array}{l} y = x – 2・・・①\\ y = -x + 14・・・② \end{array} \right. \end{eqnarray} ②に①を代入して
\[x-2=-x+14\] 文字は左辺、数字は右辺に移行すると
\[x+x=14+2\] \[2x=16\] \[x=8\] \(x=8を①に代入\)
\[y=8-2\] \[y=6\] できた。
なので点Aの座標は…
\[\bbox[pink,4px]{(8,6)}\] になるね。
つきは先生、正解っすか?

うーん。かんぺき🎊
こんな感じだね。
交点の座標を求める問題はある程度はパターンだね💡
何回も繰り返し解いておくとほぼ困らないよ✨
とりあえず△ABCだから
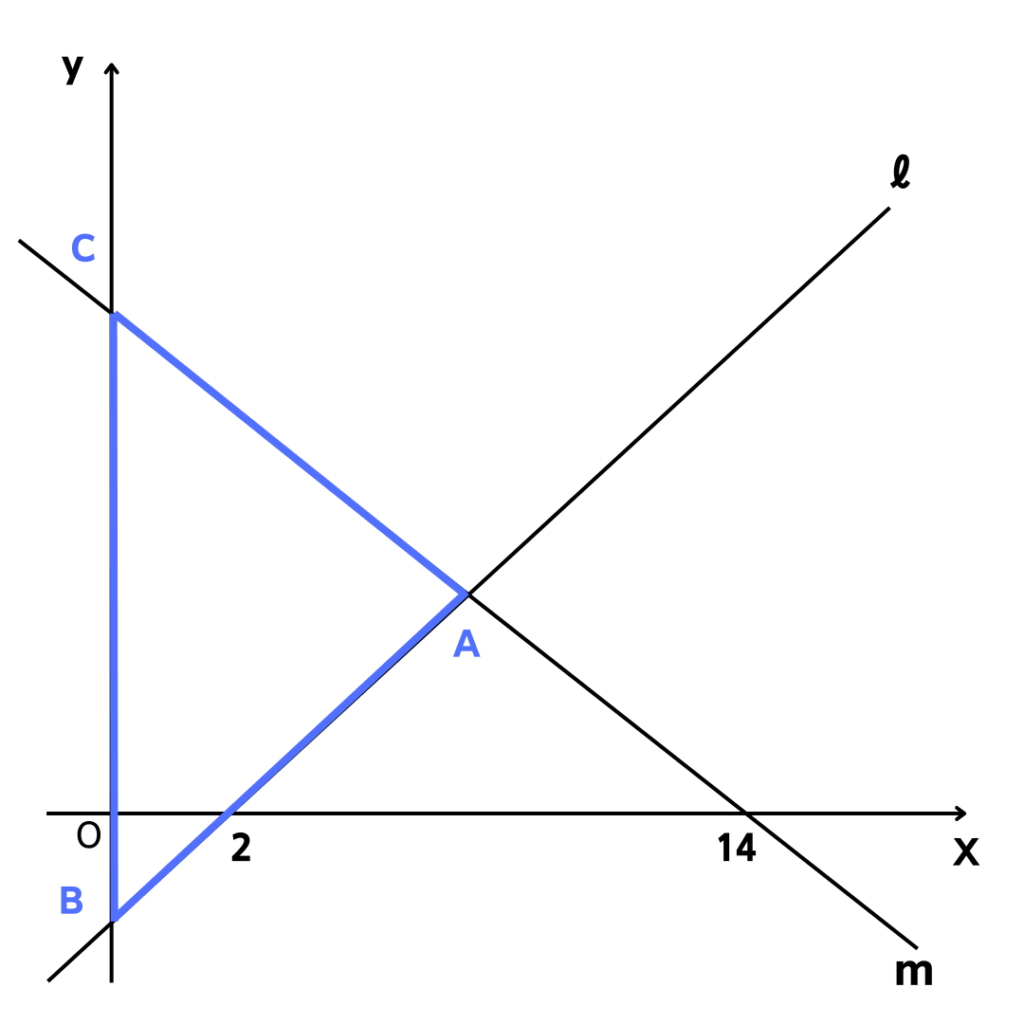
この青い三角形ってことだ…
三角形の面積だから
【底辺と高さ】が分からないとだね…
でも辺の長さがひとつもない…
つきは先生、ちょっとヒントくださいな🙏


OK👌
この三角形を見たとき、斜めになってる辺の長さは
なかなか出しにくいよ。
\(辺の長さは求めやすい❗\)
\(そして、そこを【底辺】と考えましょう。\)
\(そうすると高さも簡単に分かることが多いよ。\)
そう考えると…
うらのさん、どうなるかな❓

そっかぁ😀
じゃ、辺BCを底辺☝️
点Aから辺BCに垂線をひくとその長さが高さだね💡
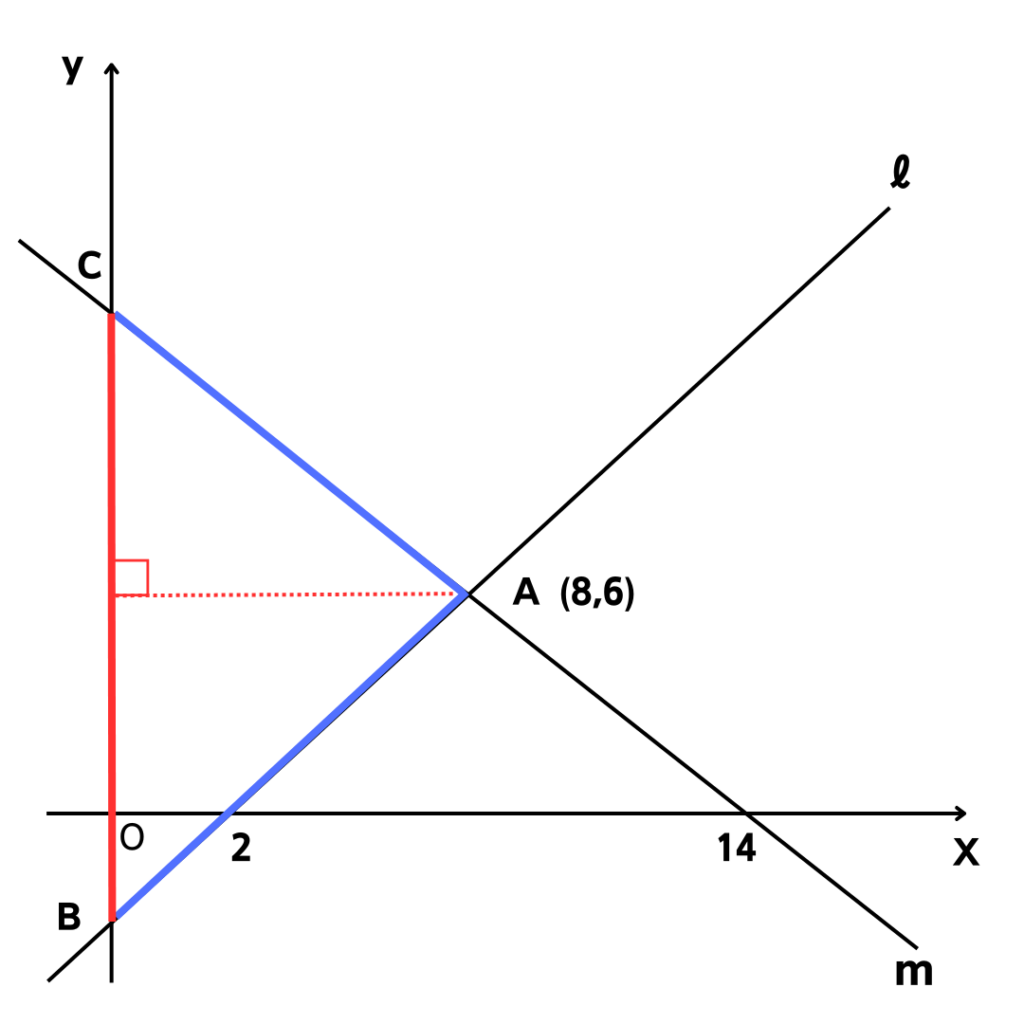
図に赤ペンで入れるとこんな感じかな。
点Aもさっきの問題で分かったから座標書き込んでみました。
……うーん。
ただ、BCの長さわかんないよ…
つきは先生、どうする❓

うん?
せっかく図に入れてみたんだから、よく見てごらん❗
BとCの座標は出せるんじゃない💡
\(直線\:ℓ\:と\:y\:軸との交点をB、\)
\(直線\:m\:と\:y\:軸との交点を\:C\:とし、\)
って書いてくれてあるじゃない。
\(\:y\:軸との交点のこと一般的になんて呼んでるっけ❓\)

切片でしょ。
…うん?切片…
あ、さっき直線の式出てるからもうわかってるはず❗
一次関数の式は…
\[直線\:ℓ\:は\:y=x-2\] \[だから、切片は-2\] \[なので、\bbox[orange,4px]{点Bの座標は(0,-2)}\]\[直線\:m\:は\:y=-x+14\] \[だから、切片は14\] \[なので、\bbox[lightgreen,4px]{点Cの座標は(0,14)}\]
こうですよね❓
つきは先生。

すばらしい✨
うらのさん、
今の情報を図のなかに書き込んでみよう🖍️
そうすると見えることもけっこうあるかもね✨

そうだね💡
やってみよう👍
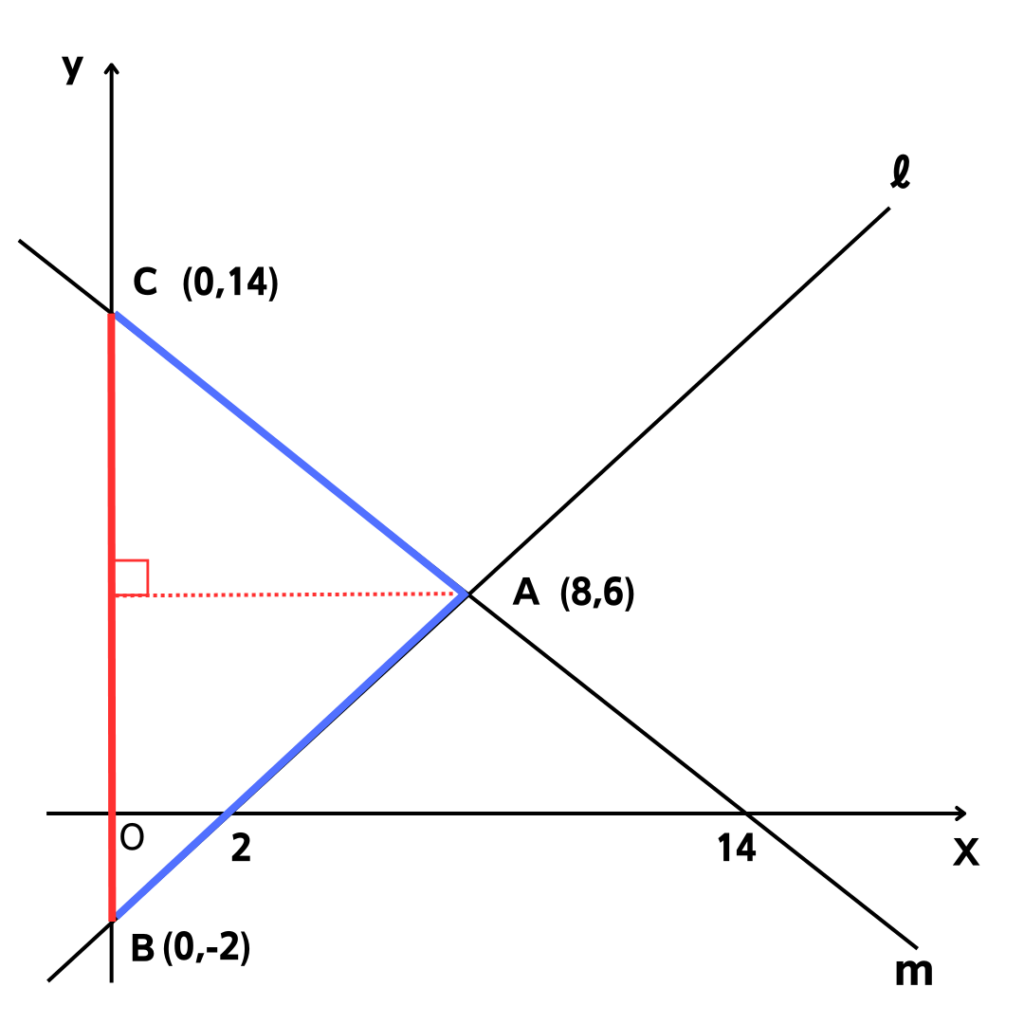
座標入れるとこうだね。
\(辺BCの長さは…\)\(点Bから点Cのy軸の長さと同じだね。\)
\(数直線で-2から14までの長さと同じ感覚なので\)
\(点Bから原点までが2、原点から点Cまでが14。\)
\(つまり、2+14=16\)
\(【辺BCの長さは16】ってことだ。\)
高さの部分はどう考えよう🤔

うん。よくできました👏
高さの赤い点線は…
\(\:x\:軸と平行だよね\)\(なら、\:x\:軸まで平行移動させたら、\)
\(同じ長さがあるんじゃないの❓\)
うらのさん、この視点で考えてみて✨

やってみましょう👍
高さの点線を平行移動させて…。
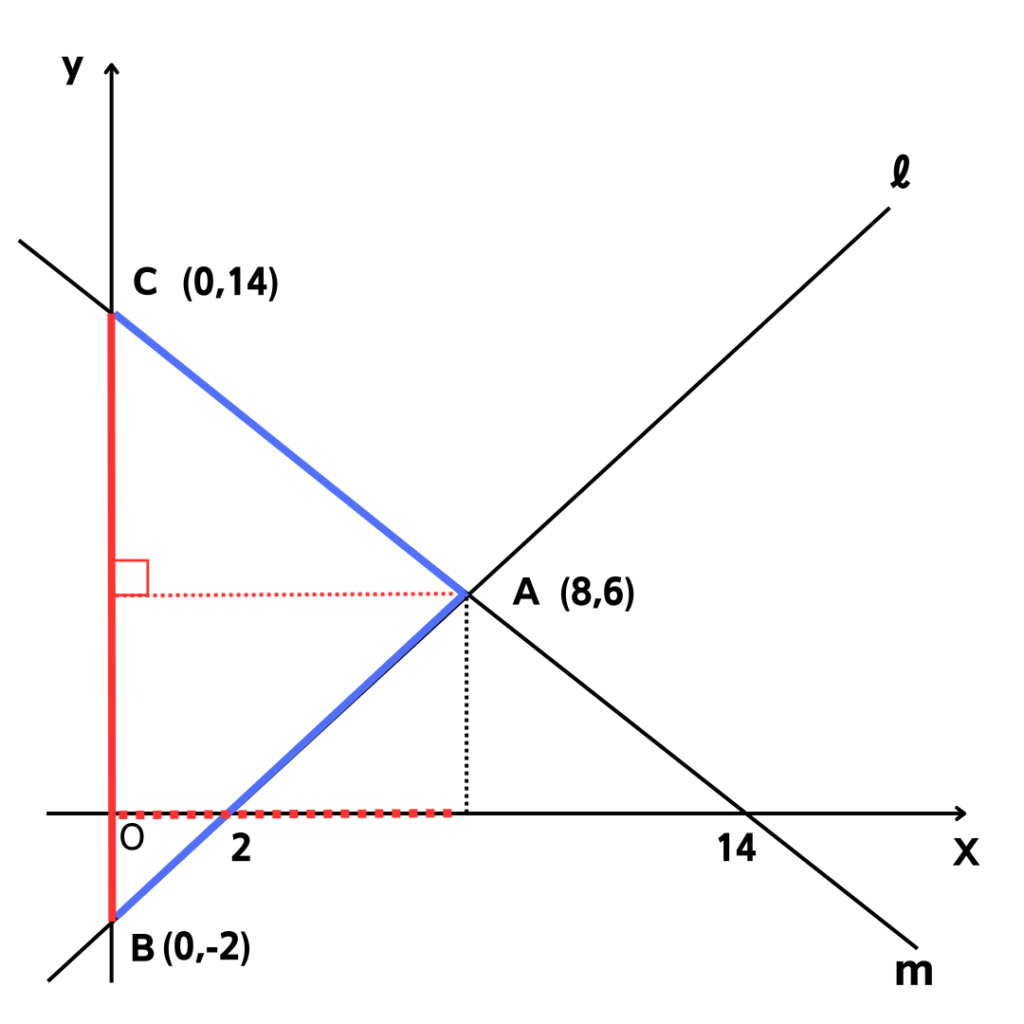
\(点Aの\:x\:軸の長さと同じだ❗\)
\(なら、【高さは8】で決まり✨\)

そうそう。そういうこと👏
では、今までの情報を図にまとめましょ❗
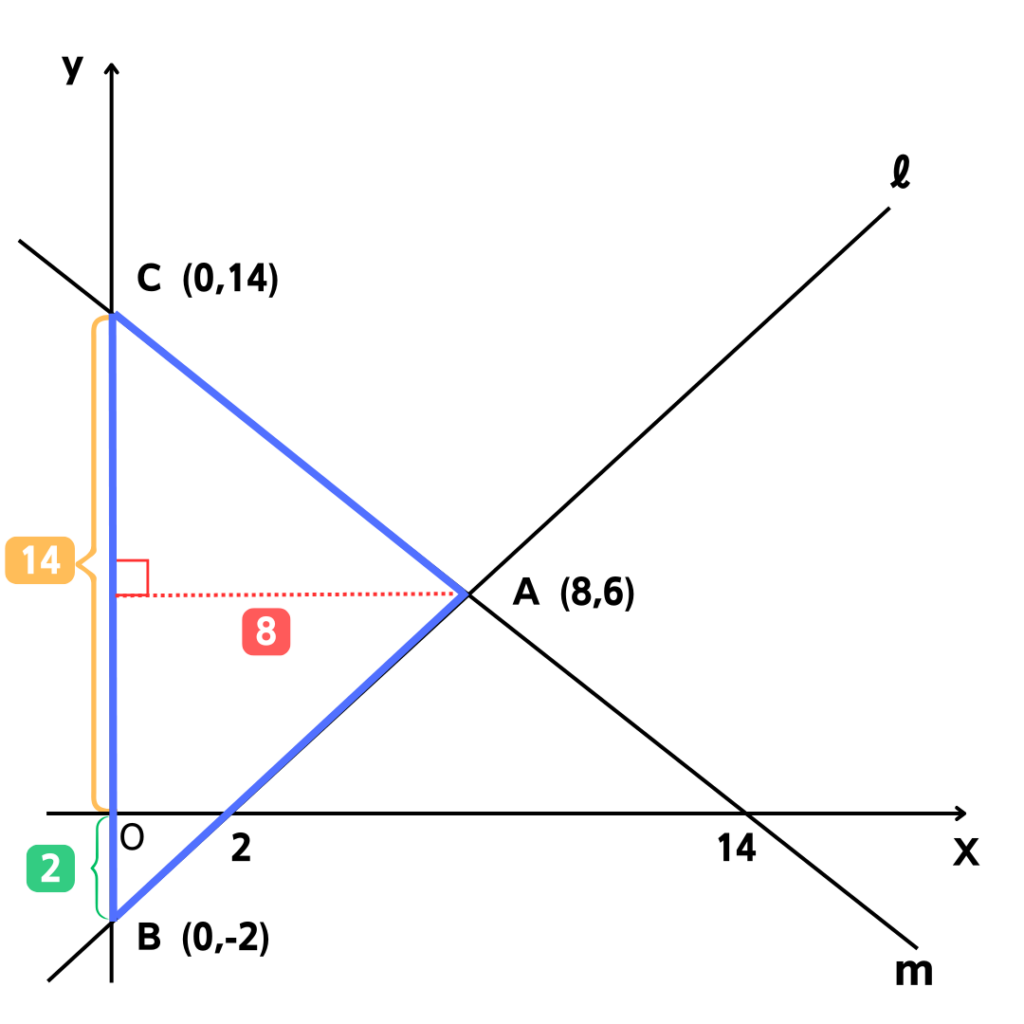
こんな感じだね。
図に書き込むとものすごく分かりやすくなるよ✨
うらのさん。
あとは三角形の面積出すだけだね👍

\[\dfrac{1}{2}\times 16\times 8=64\] だから、答えは… \[\bbox[pink,4px]{64}\] だね。

グッジョブ👍
面積はとりあえず頂点の座標を出してみる。
図形回してみながら【底辺と高さ】を決める。
これも図形のなかに情報書き込んでやってく。
そうするとぐっと分かりやすくなるよ👍
📝定期テスト対策📝
ITTO個別指導学院 長野には…
テストターボ
があります。
授業回数はチケット制🎫
入会しなくてもOK。
一度、ITTOの個別指導を体感してみてください❗
最後までお読みいただきありがとうございます🙇♀️
随時コンテンツを更新いたします❗
またお目にかかることを楽しみにしております✨








