【3月】ステップアップゼミ数学
もうすぐ春休みだね👍

今のうちに学年の復習をして
わからない問題を解決しておきたい🤚

3学期期末テストで思ったような結果が出なかった…。
そんなとき…
ITTO個別指導学院 長野の
ステップアップゼミがあるよ✨
↓詳しくはこちら↓
数学ステップアップゼミ
3月は
3月21日(土)
開催!
学年なんて関係ない!
中学生なら必要な単元を選んで参加OK👍
2つとも参加もできるよ✨
🎈川中島校・青木島校🎈
中1の単元 13:00~13:50
中2の単元 14:00~14:50
🪄篠ノ井校🪄
中1の単元 13:00~13:50
中2の単元 16:00~16:50
★お申し込みは3月13日(金)まで!★
📝受講料📝
3,010円(税込み)
3月のステップアップゼミ【数学】
中1の単元
【データの活用】
中2の単元
【箱ひげ図】
授業時間は50分
✨【とってもよくわかる解説(15分くらい)】
🖍️【問題を解く時間もたっぷり(20分くらい)】
🎉【やさしいポイント解説(15分くらい)】
3月【中1の単元】は
こんな感じの問題
📝See an Example Problem1
下の図は、あるクラスの男子の握力テストの結果をヒストグラムに表したものである。
次の問に答えなさい。
①このクラスの男子の人数は何人ですか。
②記録の高い方から数えて8番目の生徒はどの階級に属するか答えなさい。
③中央値はどの階級に属するか答えなさい。
④ヒストグラムに度数分布多角形を書き入れなさい。
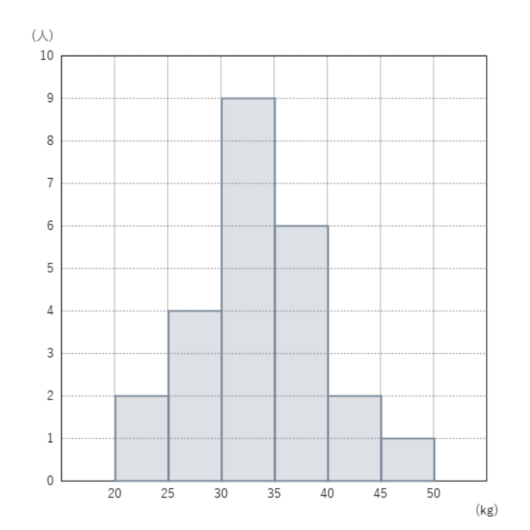
【ポイント👆】
まずはヒストグラムの読み方を確認しよう❗
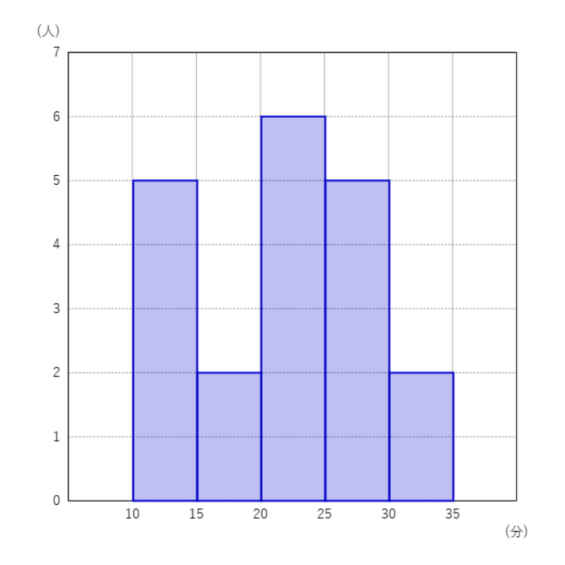
このヒストグラムはあるクラスの男子の学校から家までの通学時間です。
🤚各階級の通学時間の人数
10分以上15分未満は5人15分以上20分未満は2人…
みたいな感じでその階級の人数が分かるよ💡
🤚クラスの男子の合計人数
ヒストグラムの縦軸の人数を合計しよう。
このときは合計人数【5+2+6+5+2=20人】です。
🤚最頻値
(最も多い通学時間のこと)
この場合…
最も多いのは20分以上25分未満が6人で一番多い。
だから、20分と25分の階級の階級値(真ん中の値)の22.5分です。
【ポイント✌️】
中央値を確認しておこう!
🤚中央値は小さい方からと大きい方から
どちらから数えても同じ番目になるよ!
例えば…
全体の人数が9人の場合
小さい方からと大きい方からの5番目が同じです。
① ② ③ ④ ❺ ④ ③ ② ①
なので、❺が中央値です。
全体の人数が10人の場合
小さい方からと大きい方からの5番目が違います。
小さい方から→
① ② ③ ④ ❺ ❺ ④ ③ ② ①
←大きい方から
小さい方と大きい方から数えて、ちょうど真ん中にならない
この場合は❺+❺して÷2をしたのが中央値!
このヒストグラムは、合計の人数は20人。
だから、中央値はどちらから数えても10番目をたして÷2したもの。
どちらから数えても10番目は、20分以上25分未満の階級です。
だから、中央値は22.5分です。
合計が偶数or奇数で中央値の求め方は異なるよ🤚
偶数だと計算が必要、奇数だと計算しなくても答えは書いてあるよ!
🤚度数分布多角形の書き方
度数分布多角形は、各階級の真ん中に点をポイント。
それを定規で点を結ぶと完成。
度数のないところもしっかりと点を打つのがポイント👍
さっきのものはこんな感じですね💡
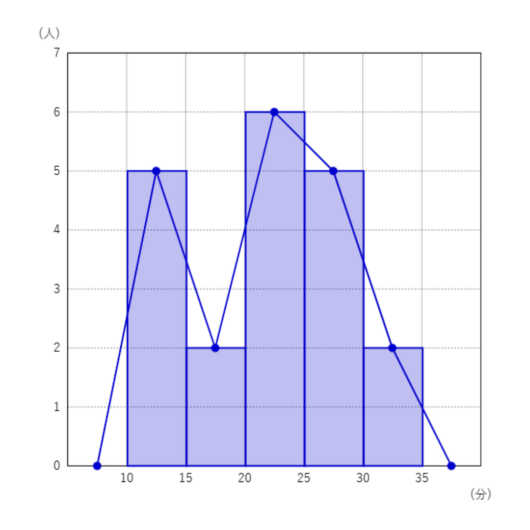
では、問題を解いてみましょう✍️
①このクラスの男子の人数は何人ですか。
ヒストグラムを見てみよう!
20kg以上25kg未満の人数は2人
25kg以上30kg未満の人数は4人
30kg以上35kg未満の人数は9人
35kg以上40kg未満の人数は6人
40kg以上45kg未満の人数は2人
45kg以上50kg未満の人数は1人
だよね。
だから、合計人数は…
2+4+9+6+2+1=24人
②記録の高い方から数えて8番目の生徒はどの階級に属するか答えなさい。
高い方から数えて8番目を考えてみるよ!
45kg以上50kg未満の人数は1人
⇒1番目は45kg以上50kg未満
40kg以上45kg未満の人数は2人
⇒2番目・3番目は40kg以上45kg未満
35kg以上40kg未満の人数は6人
つまり、8番目はこの6人のうちの高い方から5番目になるね。
よって、高い方から8番目の生徒は
35kg以上40kg未満の階級
にいるよ!
③中央値はどの階級に属するか答えなさい。
①から合計人数は、24人です。
この場合は小さい方と大きい方から数えて12番目のいる階級が中央値です。
小さい方から数えた12番目の次(13番目)が大きい方から数えた12番目です。
なので、握力のない順に12番目を考えてみます。
20kg以上25kg未満の人数は2人
👉この2人は1番目と2番目
25kg以上30kg未満の人数は4人
👉この4人は3番目~6番目
30kg以上35kg未満の人数は9人
👉この9人は7番目~15番目
そうすると…
12番目と13番目は30kg以上35kg未満の階級です。
だから、中央値は…
30kg以上35kg未満の階級に属する
これが答え👍
④ヒストグラムに度数分布多角形を書き入れなさい。
各階級の上部真ん中の部分に点を入れます。
それを、直線でつなぐことで度数分布多角形が書けます。
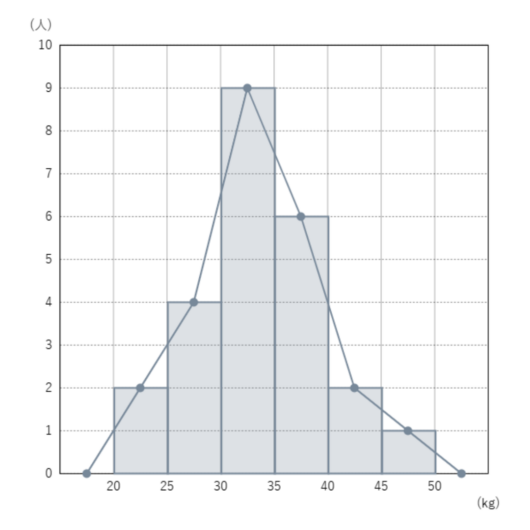
📝See an Example Problem2
下の表はある中学校の1年女子40人のハンドボール投げの記録の度数分布表です。
ア、イ、ウ、エ、オに当てはまる数を求めなさい。
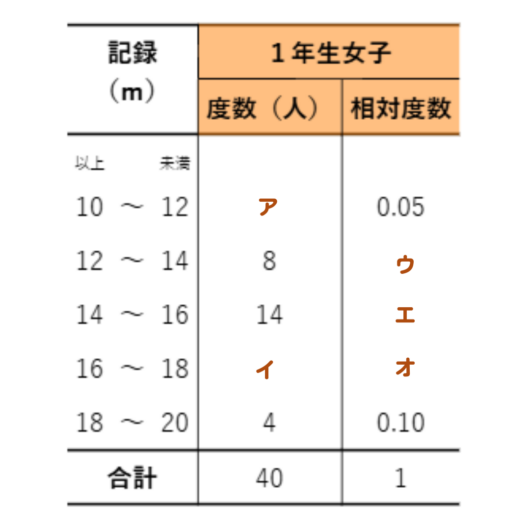
【ポイント👆】
度数分布表の読み方を確認しよう❗
🤚度数はそれぞれの階級の人数
🤚相対度数はそれぞれの階級の度数を
合計の度数でわったもの
相対度数は必ず小数で記入すること!(分数はダメですよ)
相対度数の合計は必ず1.00になるよ!
(ならなかったらどっか違ってます…)
例えば、こんな度数分布表だと…
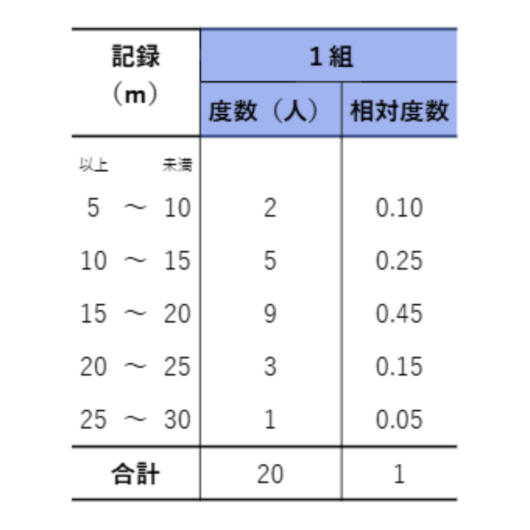
10m以上15m未満の相対度数を求めるには…
度数は5人で合計は20人。
だから、5÷20で0.25です。
では、問題を解いてみましょう✍️
まずはアからいきましょう!
合計が40人なので、合計から求められそうな感じするけど…
イが分かってないので、ちょっとムリだね…
そういうときは相対度数から考えてみよう❗
【相対度数=その階級の度数÷度数の合計】
だから
【その階級の度数=相対度数×度数の合計】
です。
だからアは…0.05×40=2
よって、アは2だよ👍
次にイを考えよう!
アは2って分かったので
全部の度数の合計からイ以外の度数の合計をひけばOK✨
だから…
40-(2+8+14+4)=12
よって、イは12です👍
さらに、ウ・エ・オにいこう。
これは相対度数です。
だから…
【相対度数=その階級の度数÷度数の合計】
で計算できます!
ウ…8÷40=0.20
エ…14÷40=0.35
オ…12÷40=0.30
よって…
ウは0.20、エは0.35、オは0.30
になるね👍
相対度数も分からないものが一個だったら
合計からその他の合計をひけば出せるよ💡
こういう問題は、解く順番もポイントになることもあるよ。
なので、解けないものはとばしておいて、他の解けそうなところから解けばいいよ。
そうすると一度解かなかったところも解けてくることが多いよ👍
3月【中2の単元】は
こんな感じの問題
📝See an Example Problem
ある中学校の中1生13人と中2生13人の期末テストの数学(100点満点)の得点の箱ひげ図です。
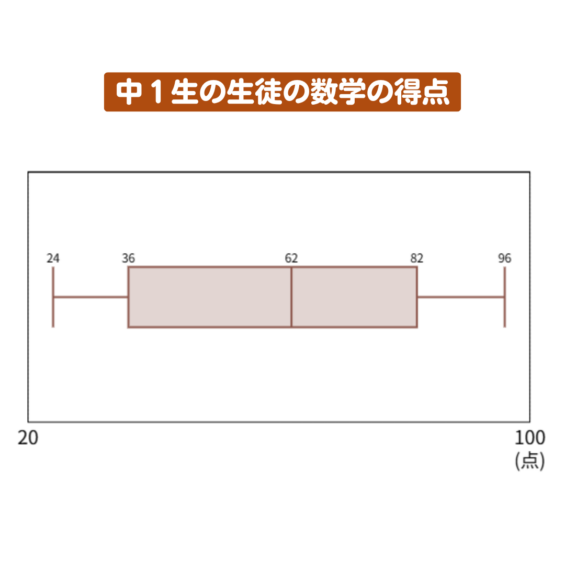
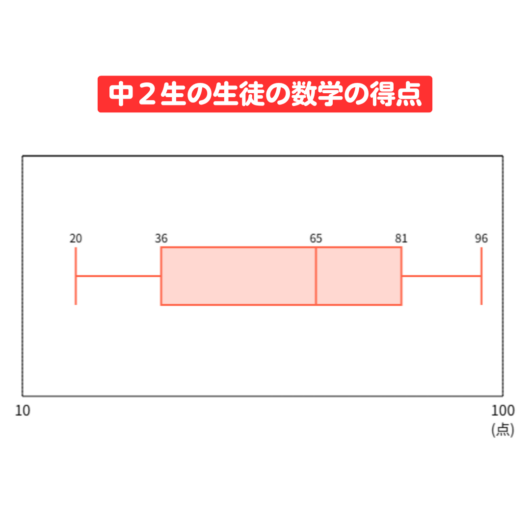
①この箱ひげ図から、次の表を埋めなさい
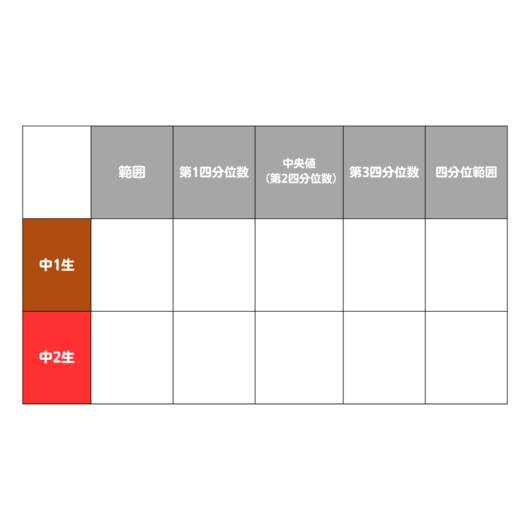
②この箱ひげ図から読み取れるもので、確実に言えるものを一つ選びなさい。
ア 65点以上の人は中1生、中2生ともに6人以上はいる
イ 62点以下の人は中1生、中2生ともに6人以上はいる
ウ 62点以上の人は中1生、中2生ともに6人以上はいる
③中1生、中2生の箱ひげ図から考えられる中1生と中2生の適当なデータを
A~Dからひとつずつ選びなさい。
A:24 34 34 37 45 51 62 63 73 80 83 92 96 (点)
B:24 33 35 37 44 53 62 69 72 81 83 91 96 (点)
C:20 31 35 39 46 55 65 70 74 80 83 92 96 (点)
D:20 30 34 38 45 55 65 70 73 80 82 93 96 (点)
【ポイント👆】
箱ひげ図の読み方を確認しておこう❗
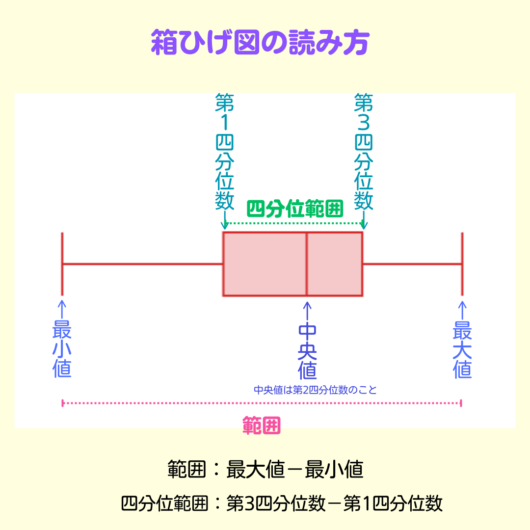
データを大きさ順に並べて、4等分する値が四分位数です。
だから、箱ひげ図の縦線はデータを4等分で、各線の間には同じ個数のデータがあります。
人数が奇数と偶数の場合で考え方がちょっと違います。
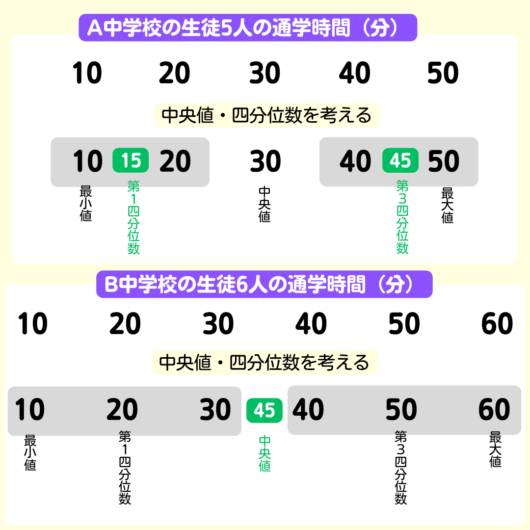
四分位数や中央値は小数になることも多いです。
小数になっても間違ってないので、気にしない👍
では、問題を解いてみましょう✍️
①この箱ひげ図から、次の表を埋めなさい
まずは、中1生の箱ひげ図を考えてみよう!
範囲は…
【最大値ー最小値】だから
96-24=72
第1四分位数は…
もう書いてあるね✨
箱の左の線だから36
第2四分位数は…
箱の中央の線だから62
第3四分位数は…
箱の右の線だから82
四分位範囲は…
【第3四分位数-第1四分位数】なので
82-36=46
中2生も同様に考えてみよう!
範囲は…
【最大値ー最小値】だから
96-20=76
第1四分位数は…
こっちも書いてあるね✨
箱の左の線だから36
第2四分位数は…
箱の中央の線だから65
第3四分位数は…
箱の右の線だから81
四分位範囲は…
【第3四分位数-第1四分位数】なので
81-36=45
答えをまとめると下の表になるよ!
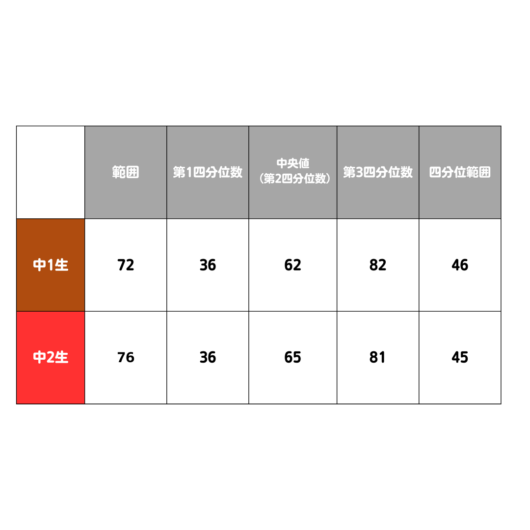
②この箱ひげ図から読み取れるもので、確実に言えるものを一つ選びなさい。
ア 65点以上の人は中1生、中2生ともに6人以上はいる
イ 62点以下の人は中1生、中2生ともに6人以上はいる
ウ 62点以上の人は中1生、中2生ともに6人以上はいる
箱ひげ図をデータの個数でまとめてみたよ👍
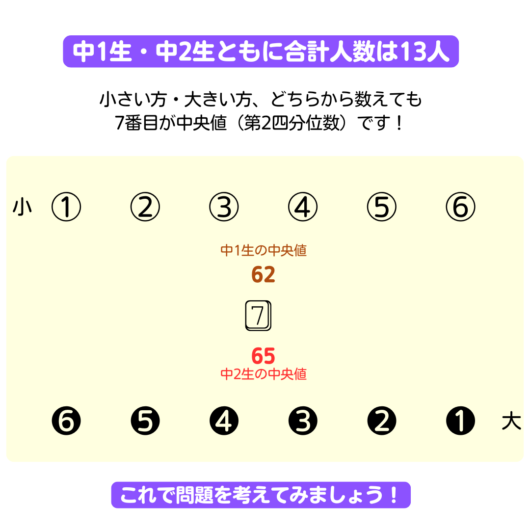
まずは、以上、以下の言葉の意味から。
以上と以下はその数を含むから、それは確認しておこう!
アから考えると…
中1生の中央値が62点なので、7番目が62点ってことになるよね。
なので、62点以上の生徒が7人は絶対います。
ただ、❻の点数が65点以上じゃないと、6人いるってことにはならないよね。
この図からだと❻は62点以上としか分からないので、アは不正解。
ちなみに…
中2生は中央値が65点なので65点以上の生徒が確実に7人はいます。
イを考えよう。
中1生の中央値が62点なので、7番目が62点ってことになるよね。
なので、62点以下の生徒が7人は絶対います。
中2生の中央値は65点なので65点以下の生徒が確実に7人はいます。
ただ、こちらも⑥が62点とは確実に分からないので、イも不正解。
ウを考える。
中1生の中央値が62点なので、7番目が62点ってことになるよね。
なので、62点以上の生徒が7人は絶対います。
中2生は中央値が65点なので65点以上の人が確実に7人はいます。
なので62点以上の生徒が確実に7人はいるよね。
よって、ウが正解!
データの個数が少ないものは書いてみる✨
目でみて分かるようにするのが大事👍
③中1生、中2生の箱ひげ図から考えられる中1生と中2生の適当なデータを
A~Dからひとつずつ選びなさい。
A:24 34 34 37 45 51 62 63 73 80 83 92 96 (点)
B:24 33 35 37 44 53 62 69 72 81 83 91 96 (点)
C:20 31 35 39 46 55 65 70 74 80 83 92 96 (点)
D:20 30 34 38 45 55 65 70 73 80 82 93 96 (点)
箱ひげ図を書くには…
最小値・最大値・中央値(第2四分位数)
第1四分位数・第3四分位数が必要だよ。
A~Dのそれらの数字をまとめてみたよ👍
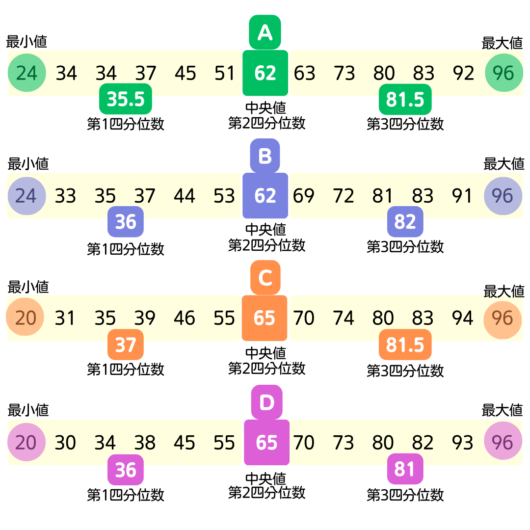
これでもうわかっちゃう!
あとはそれぞれの箱ひげ図とあわせてみよう!
中1生:B・中2生:D
だね✨
最小値と最大値は計算しなくてもすぐ出るから。
そこである程度どれか絞り込んでから詳しく見てみるといいね。
今回の授業はこんな感じの問題を一緒に解いていきます!
両方の授業を受けると
データの関連性が分かっていいよ✨
ITTO長野のホームページでは
学習にまつわるコンテンツを随時更新中🎉
またお目にかかること楽しみにしております✨







