【※受付終了12月】ステップアップゼミ数学
2学期のテスト終了!

期末テストが思ったより、点数ゲットできなかった…😫
どうしよう…💦

テストでできない問題けっこうあったな💦
今のうちに解決したい💡
そんなとき…
ITTO個別指導学院 長野の
ステップアップゼミがあるよ✨
↓詳しくはこちら↓
数学ステップアップゼミ
12月は
12月27日(土)
開催!
学年なんて関係ない!
中学生なら必要な単元を選んで参加OK👍
2つとも参加もできるよ✨
🎈川中島校・青木島校🎈
中1の単元 13:00~13:50
中2の単元 14:00~14:50
🪄篠ノ井校🪄
中1の単元 13:00~13:50
中2の単元 16:00~16:50
★お申し込みは12月19日(金)まで!★
📝受講料📝
3,010円(税込み)
12月のステップアップゼミ【数学】
中1の単元
【平面図形・作図】
中2の単元
【平行四辺形の性質】
【平行四辺形になるための条件】
授業時間は50分
✨【とってもよくわかる解説(15分くらい)】
🖍️【問題を解く時間もたっぷり(20分くらい)】
🎉【やさしいポイント解説(15分くらい)】
12月【中1の単元】はこんな感じの問題
📝See an Example Problem1
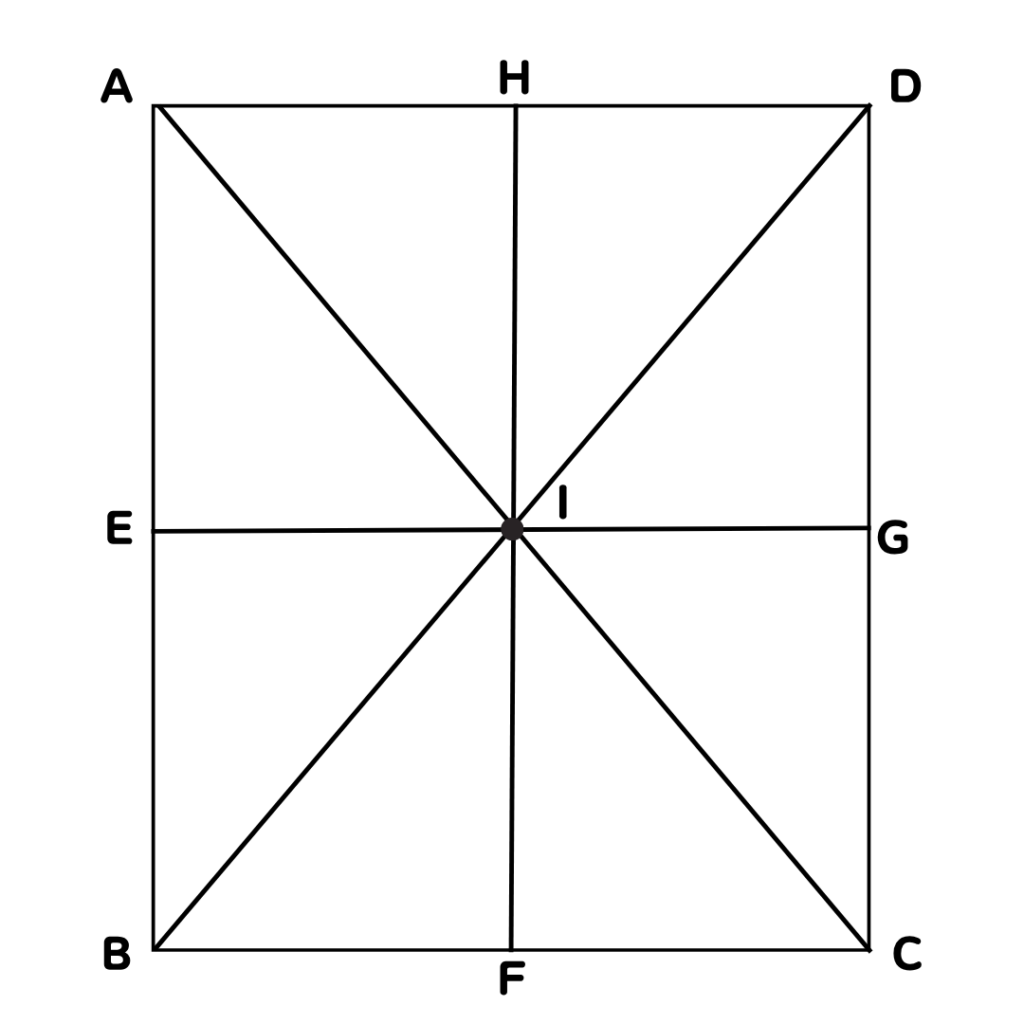
下の図は、長方形ABCDの内部を8個の合同な三角形に分けたものである。
次の問いに答えなさい。
①△AEIを平行移動させると重なる三角形をすべて答えなさい。
②点Iを回転の中心として△DGIを回転移動させると重なる三角形をすべて答えなさい。
③△IHAを1回だけ対称移動させると重なる三角形をすべて答えなさい。
【ポイント✨】
図形の移動のしかたを確認しよう❗
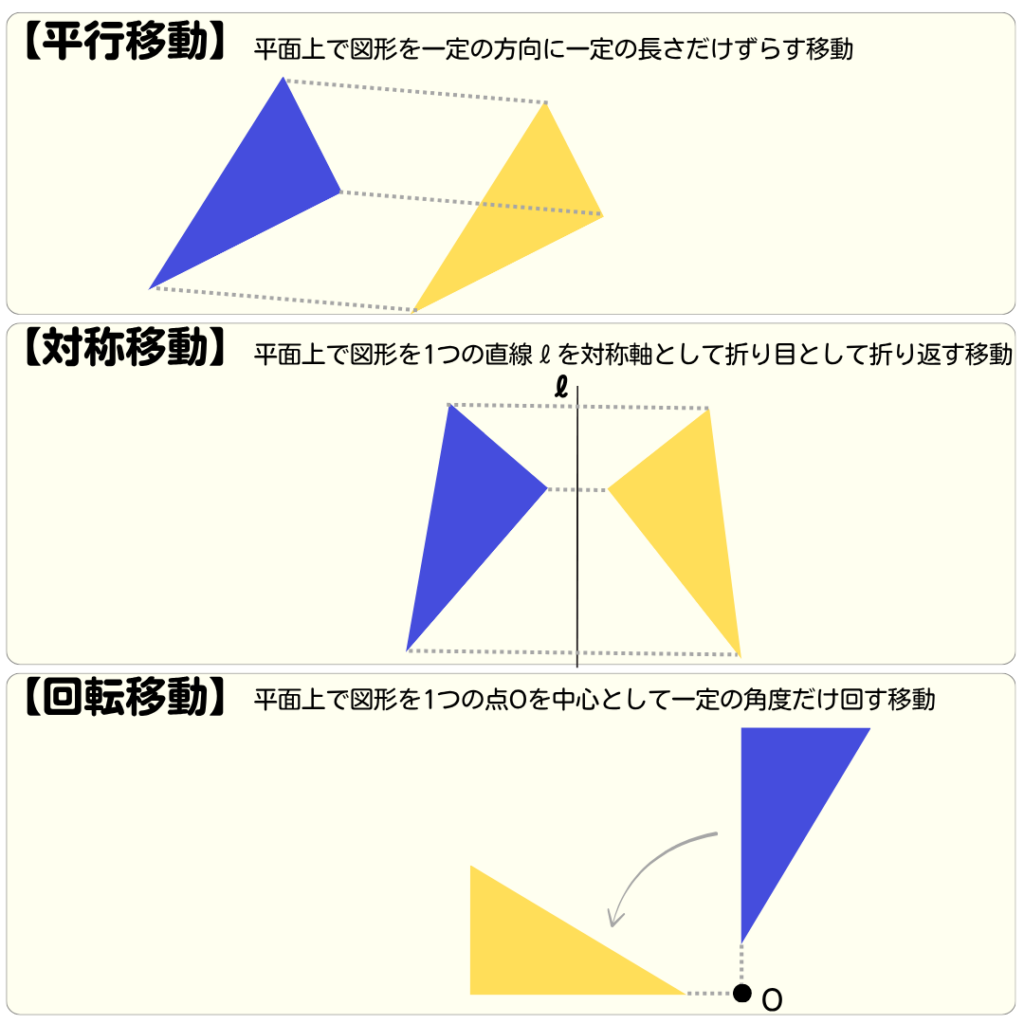
①△AEIを平行移動させると重なる三角形を
すべて答えなさい。
まずは、△AEIを確認しよう👍
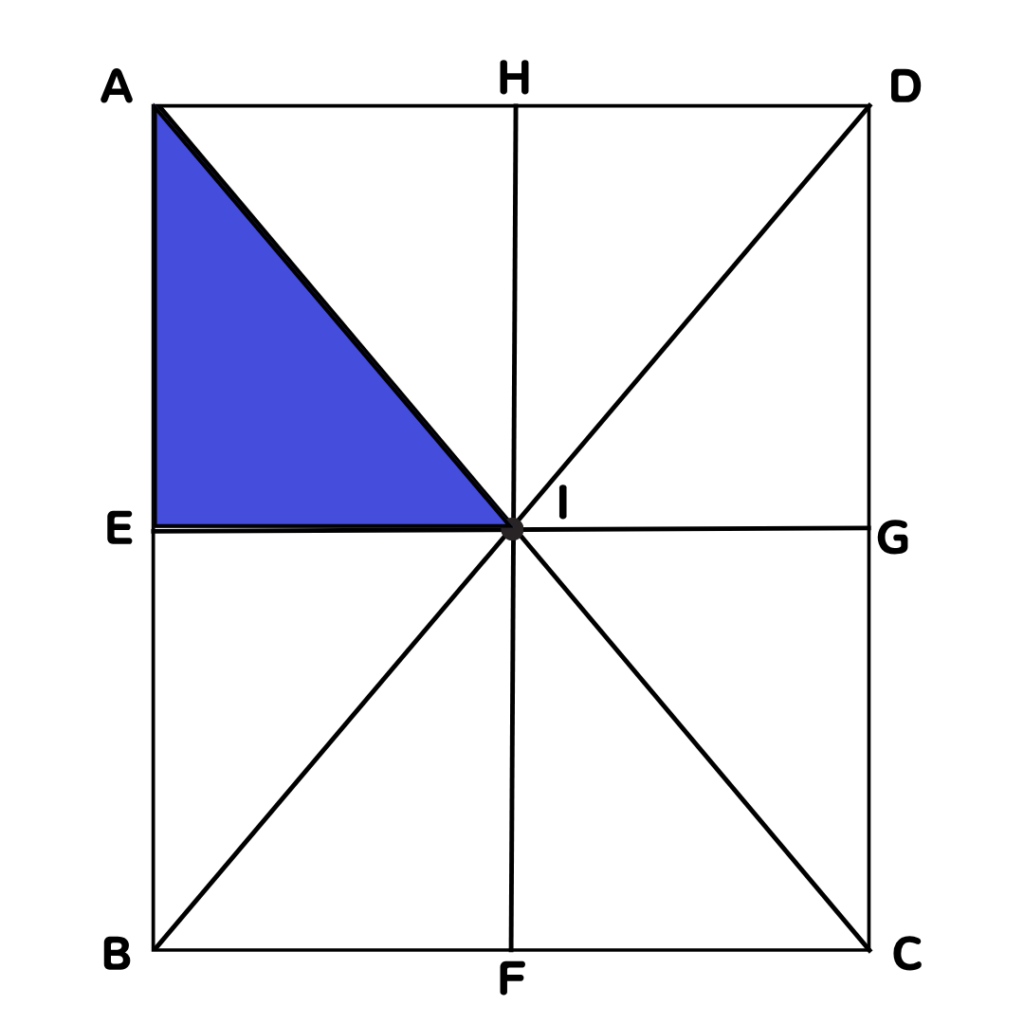
ここから、△AEIを一定の方向に同じ長さだけ
移動させて重なる三角形を考えてみよう💡
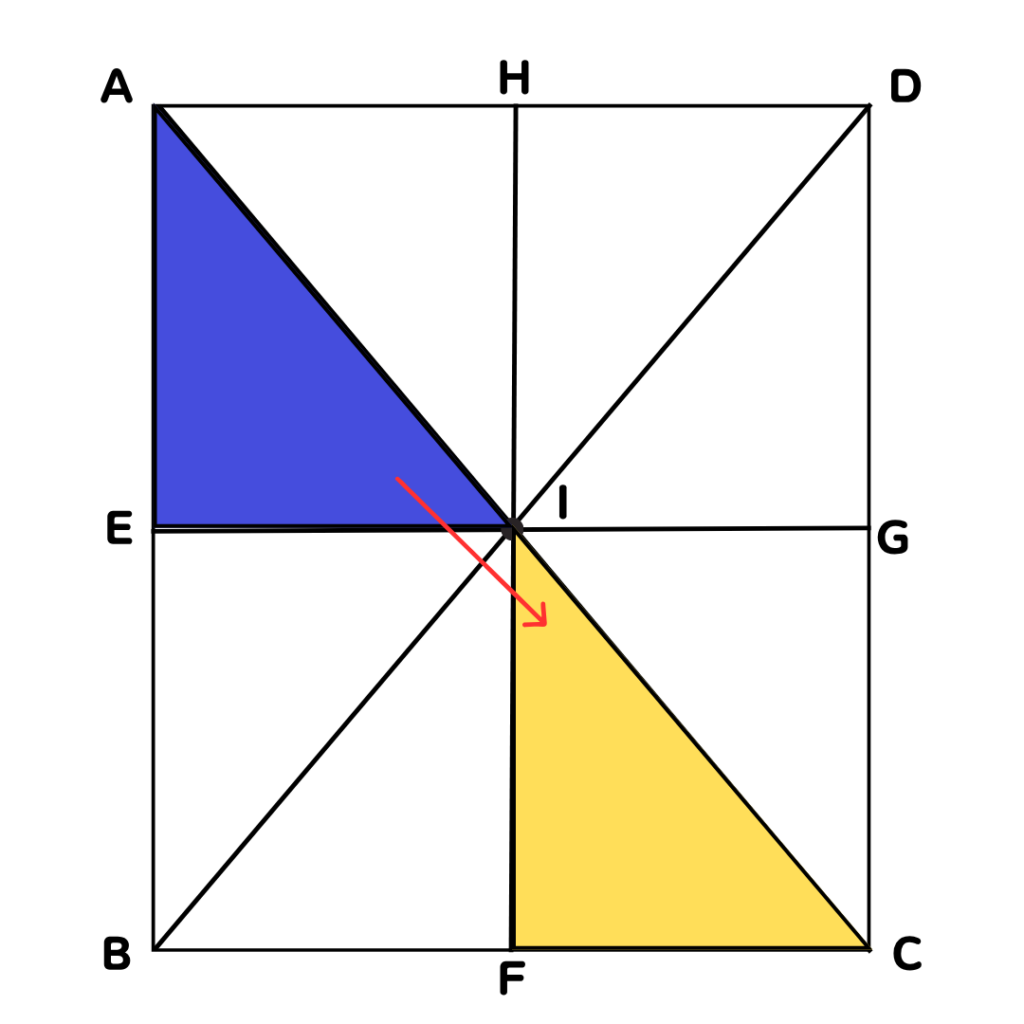
A→I・E→F・I→Cの方向に移動させると
△IFCがぴったり重なります。
それ以外のあらゆる方向に
スライドさせても重なる図形はありません。
慣れないうちは三角定規とかを動かして
実際に移動させてみるといいね👍
答えは△IFCだね。
②点Iを回転の中心として△DGIを回転移動
させると重なる三角形をすべて答えなさい。
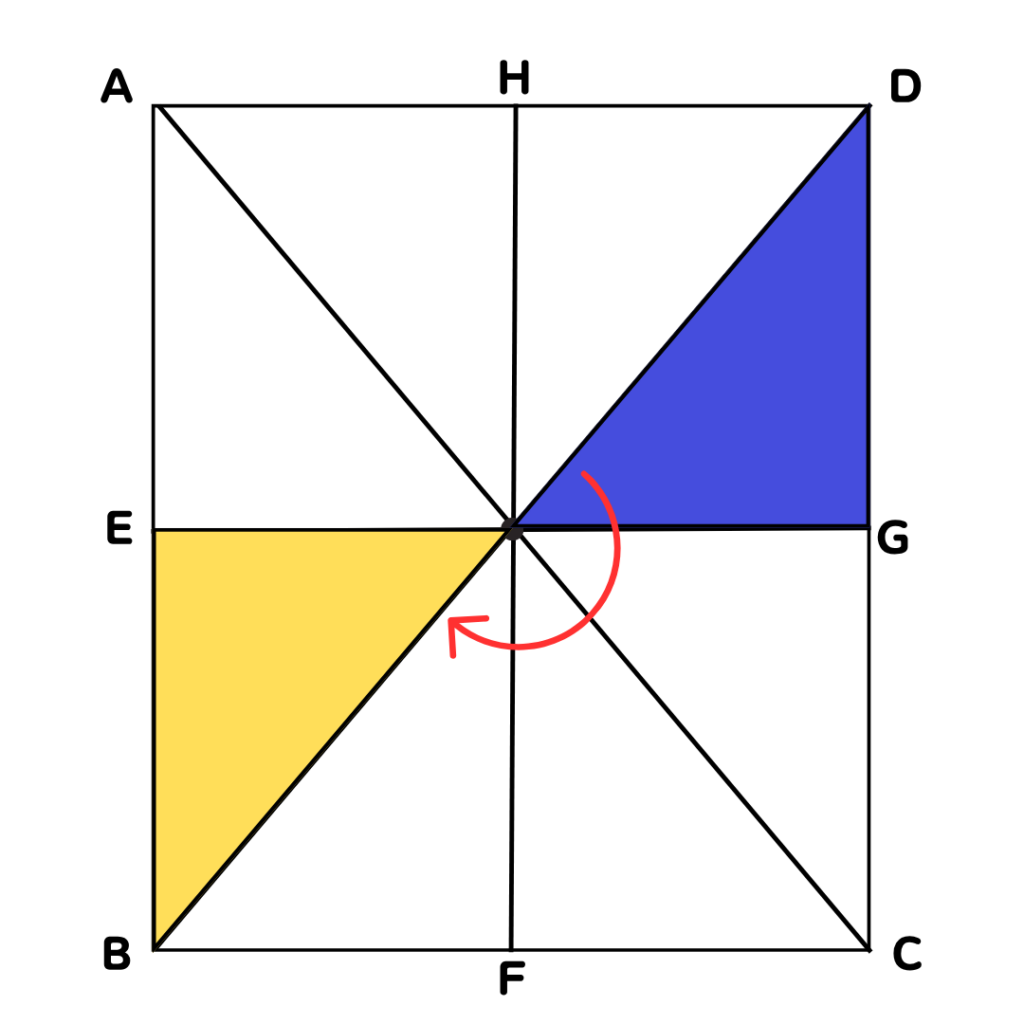
点Iを中心に180°時計回りに回転してみると…
D→B・G→Eにそれぞれ移動させると
△BEIがぴったり重なります💡
それ以外は1回転するまでに
重なる図形がありません。
答えは△BEIです。
③△IHAを1回だけ対称移動させると
重なる三角形をすべて答えなさい。
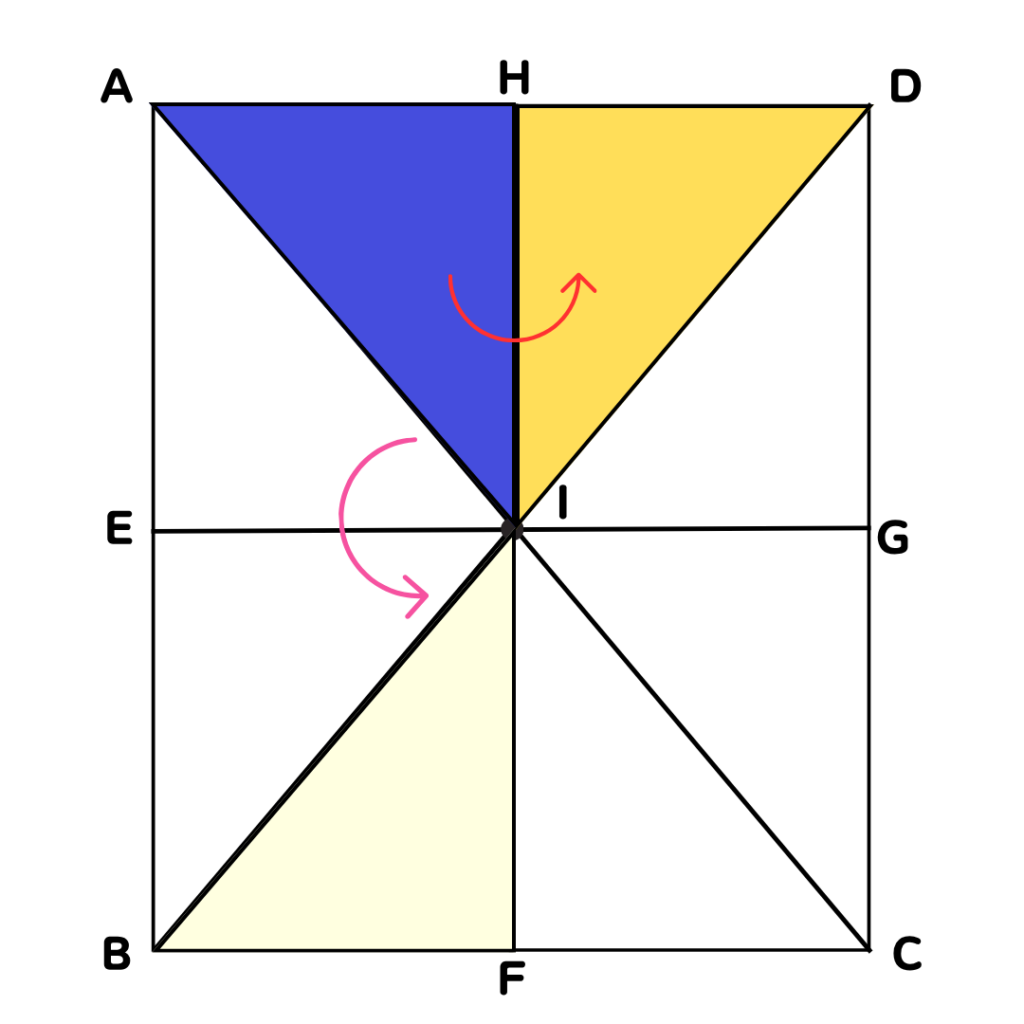
線分HFを対称の軸とすると重なるのは△IHD
線分EGを対称の軸とすると重なるのは△IFB
答えは△IHDと△IFBです。
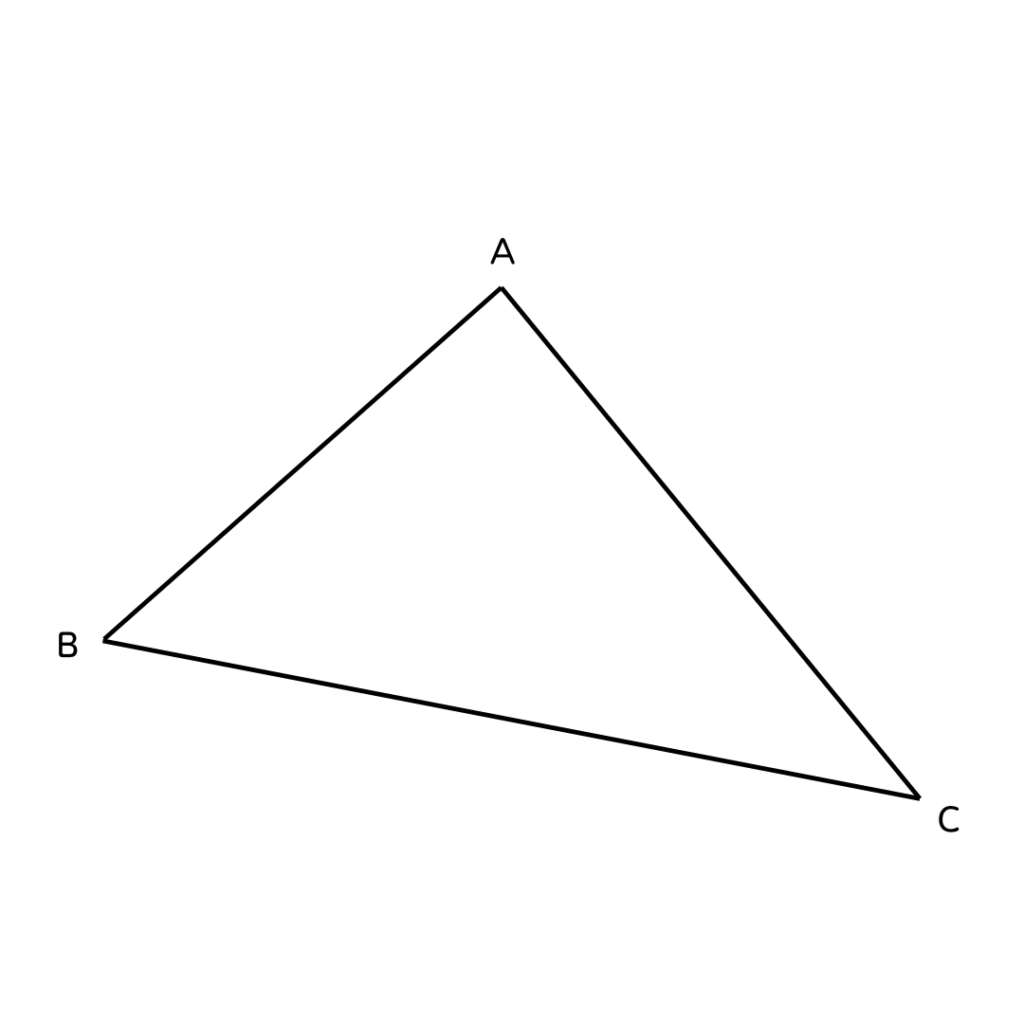
📝See an Example Problem2
下の図のような三角形ABCがある。
この三角形の∠ABCを2等分する直線上に
円の中心があり、点A、Cを通る
円の中心Oを作図しなさい。
ただし、作図で書いた線は消さないこと。
【ポイント✨】
この問題で使う作図だよ。
一度、復習しておこう👍
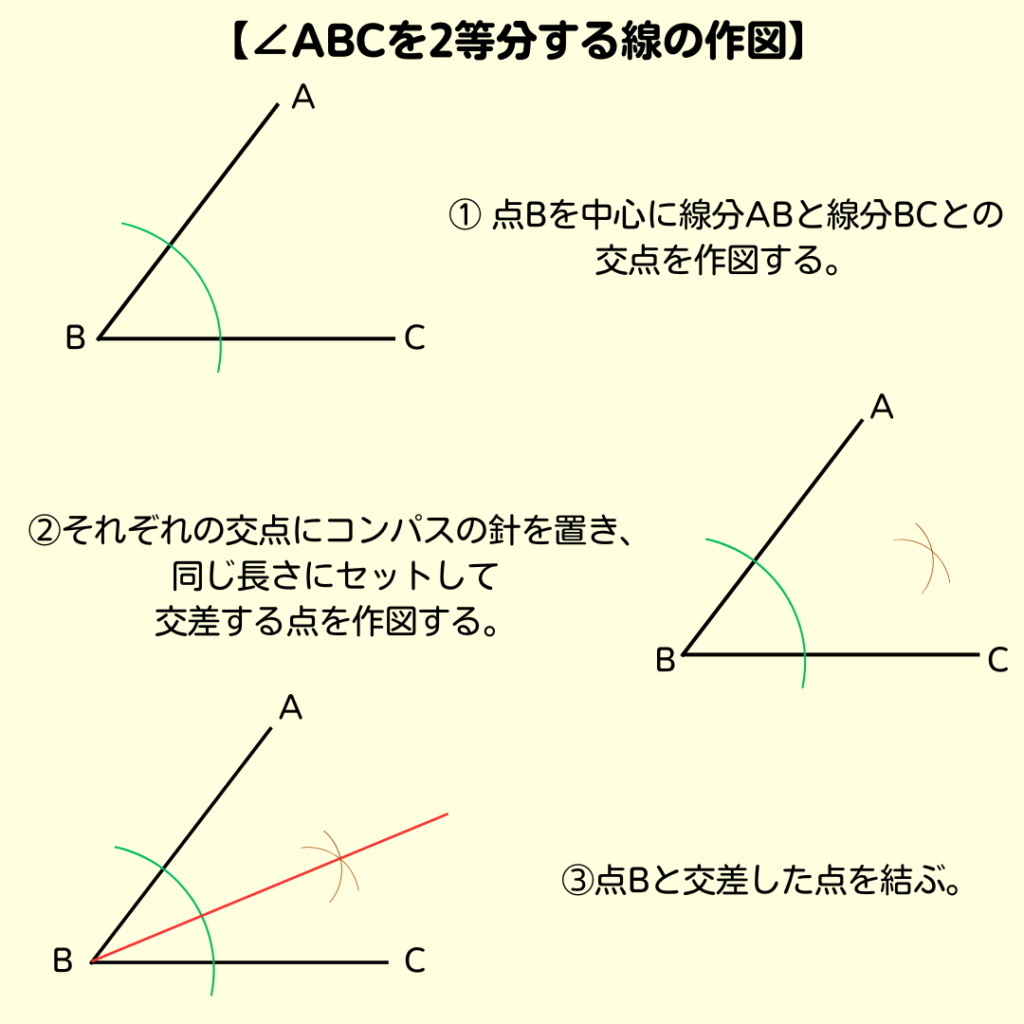
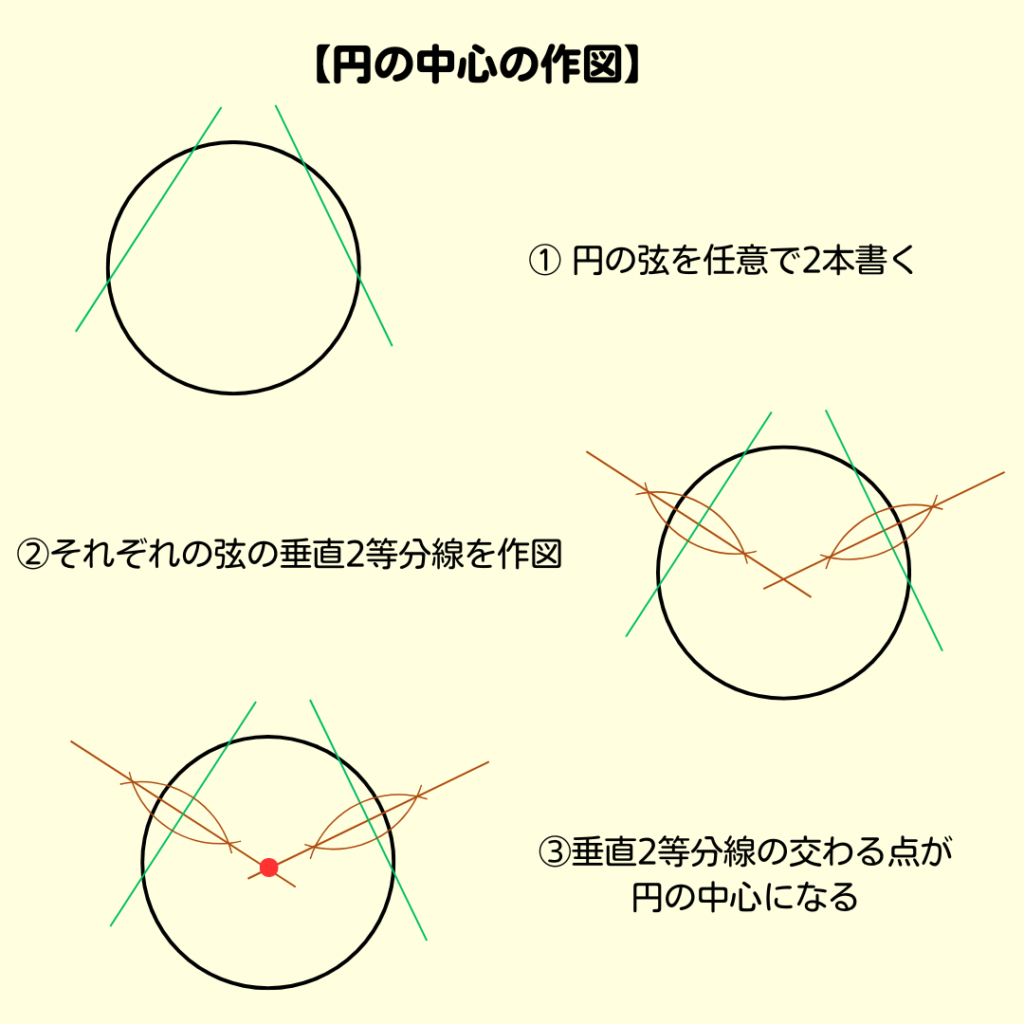
まずは…
∠ABCの2等分線を作図してみよう🖍️
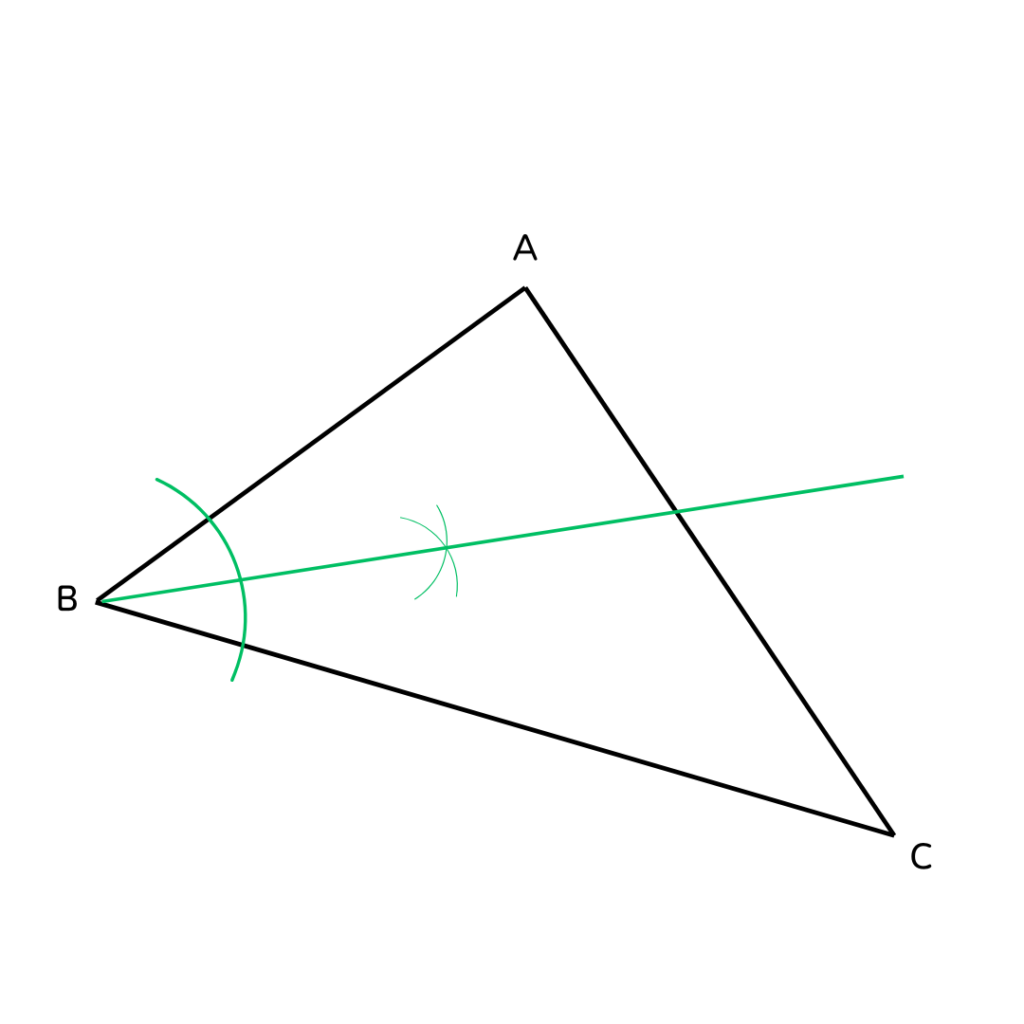
問題文から、円の中心はこの2等分線上にあるよ🤔
つぎに、点A、Cを通る円ってことなので…
線分ACを円の弦と考えれば、
円周の上に点Aと点Cがあることになるね💡
なので…
線分ACの垂直2等分線を作図してみよう📏
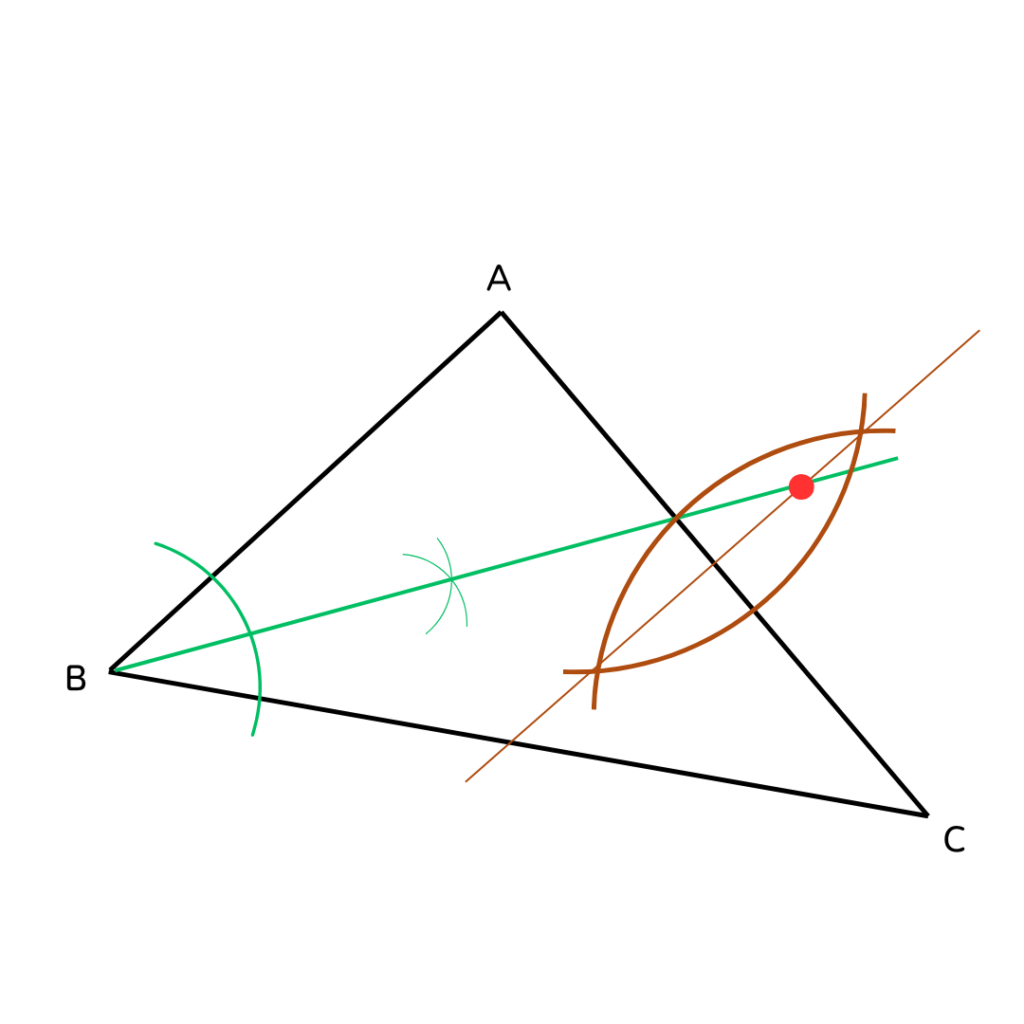
∠ABCの2等分線と線分ACの交差する点が
円の中心だね❗
この作図の場合は…
円の中心がある指定角度の2等分線上と
円の弦の垂直2等分線上にあるという
問題文から作図しよう。
12月【中2の単元】はこんな感じの問題
📝See an Example Problem1
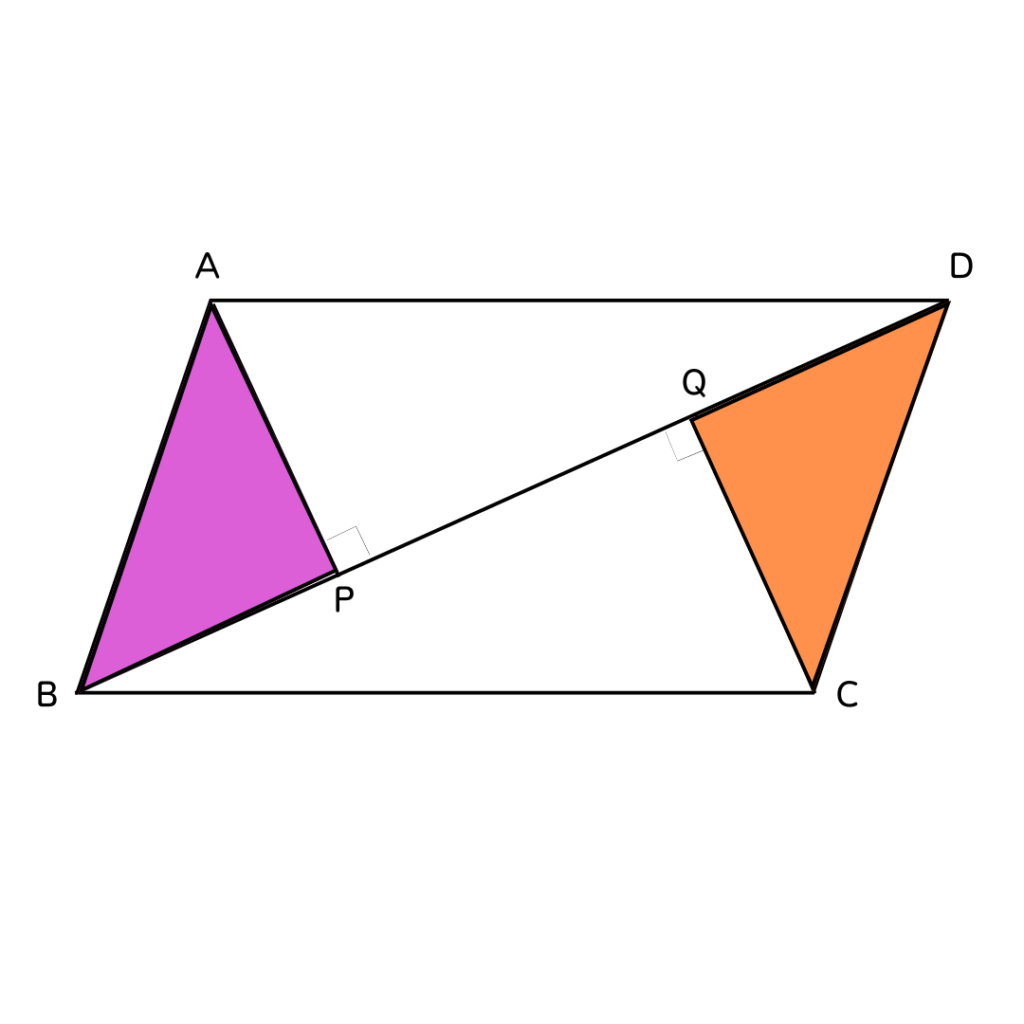
下の図のように、平行四辺形ABCDの頂点A、Cから対角線BDに垂線をひき、
BDとの交点をそれぞれP、Qとする。
このとき、AP=CQであることを証明せよ。
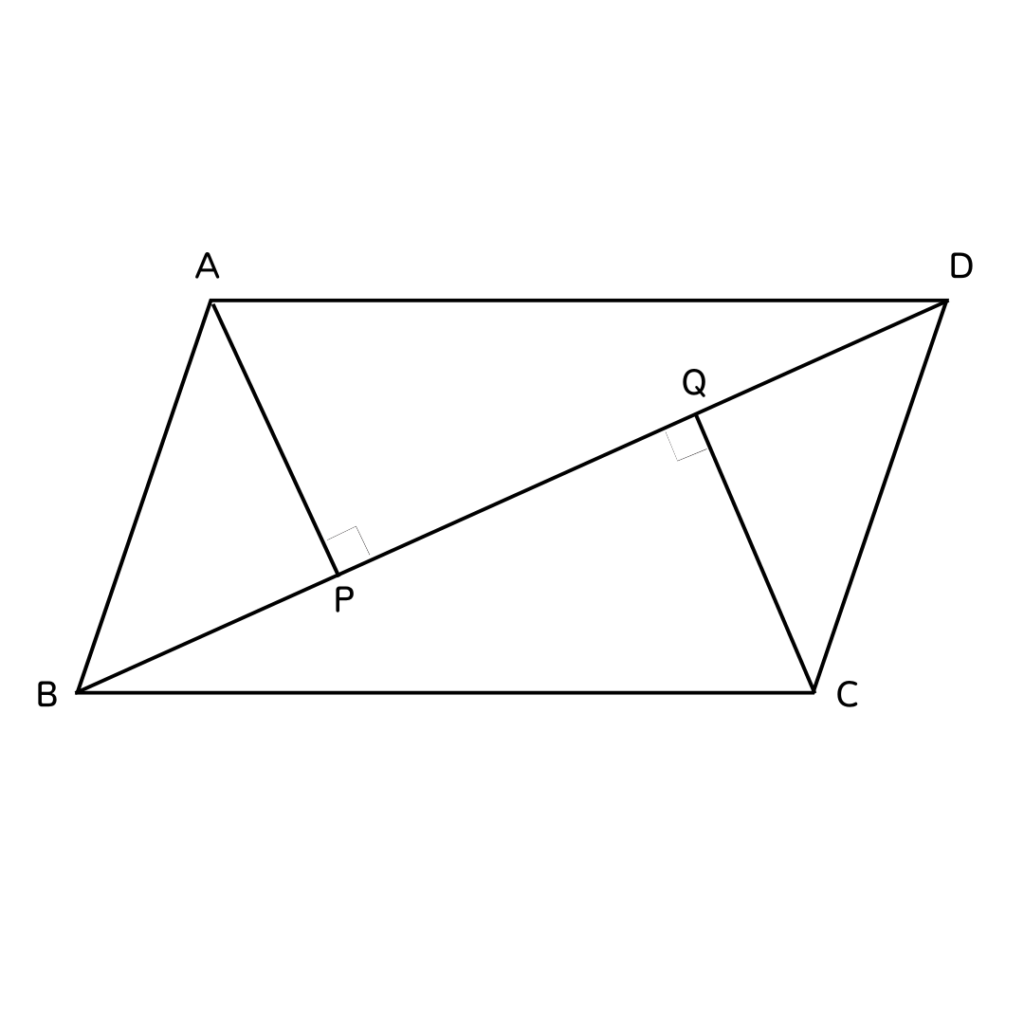
【ポイント✨】
こういう問題は三角形の合同の証明を
使うことが多いよ。
辺や角の大きさが等しいことの根拠に
平行四辺形の性質が使われることが多いよ💡
ここでは平行四辺形の性質を確認しておこう❗
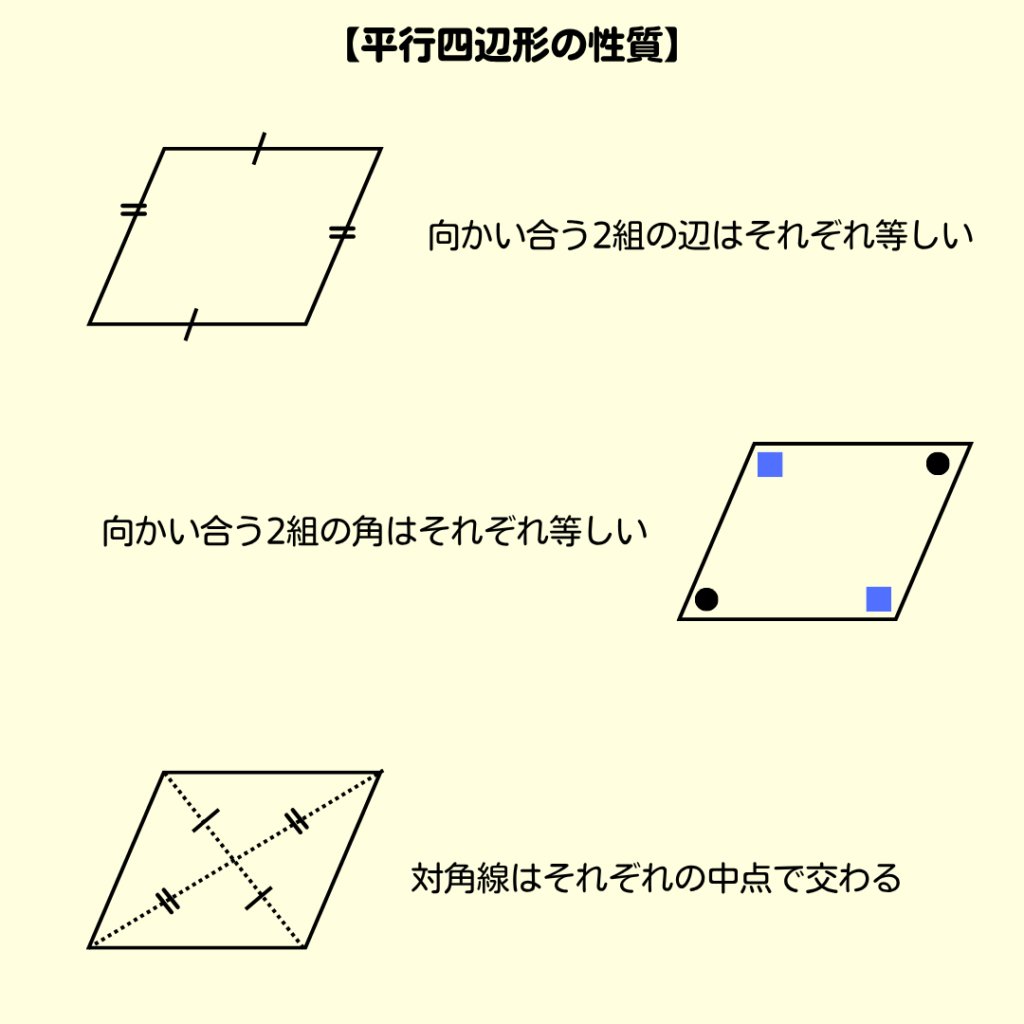
もうひとつ☝️
三角形の証明の手順も確認しておこう💡
【こんな感じで証明してみよう】
【ステップ1】
平行四辺形の性質を使って、
どの三角形とどの三角形を証明するかを書く
【ステップ2】
文章や図から根拠を3つ探して、書いていこう✍️
それぞれ番号をふっておくこと🖍️
【ステップ3】
根拠3つから、三角形の合同条件を書こう✍️
【ステップ4】
証明したい三角形を≡マークを使って表示をする
△○○○≡△●●●
【ステップ5】
長さや角度が等しいことを証明したい場合は、
「合同な図形は対応する辺(または角)が
それぞれ等しいので」
を書いてから結論を書く✍️
では、実際に進めてみましょう✍️
では、ステップにそって進んでいこう👍
証明したいのはAP=CQだよね。
関係する三角形を考えると
△APBと△CQDだね。
【ステップ1】
△APBと△CQDにおいて
【ステップ2】
問題文に垂線をひいてとありますね。
だから、これは仮定で使えそうです。
仮定より ∠APB=∠CQD=90°…①
平行四辺形の性質が使えるものは2つあるよ。
一つ目は平行四辺形の向かい合う辺は等しい。
だから、AB=CDです。
書くときは…
平行四辺形の向かい合う辺は等しいので
AB=CD…②
なんか直角三角形の合同条件が使えそうな気配。
「斜辺と他の一辺がそれぞれ等しい」
「斜辺と一つの鋭角がそれぞれ等しい」
どちらかが図を見て言えそうか考えてみよう🤔
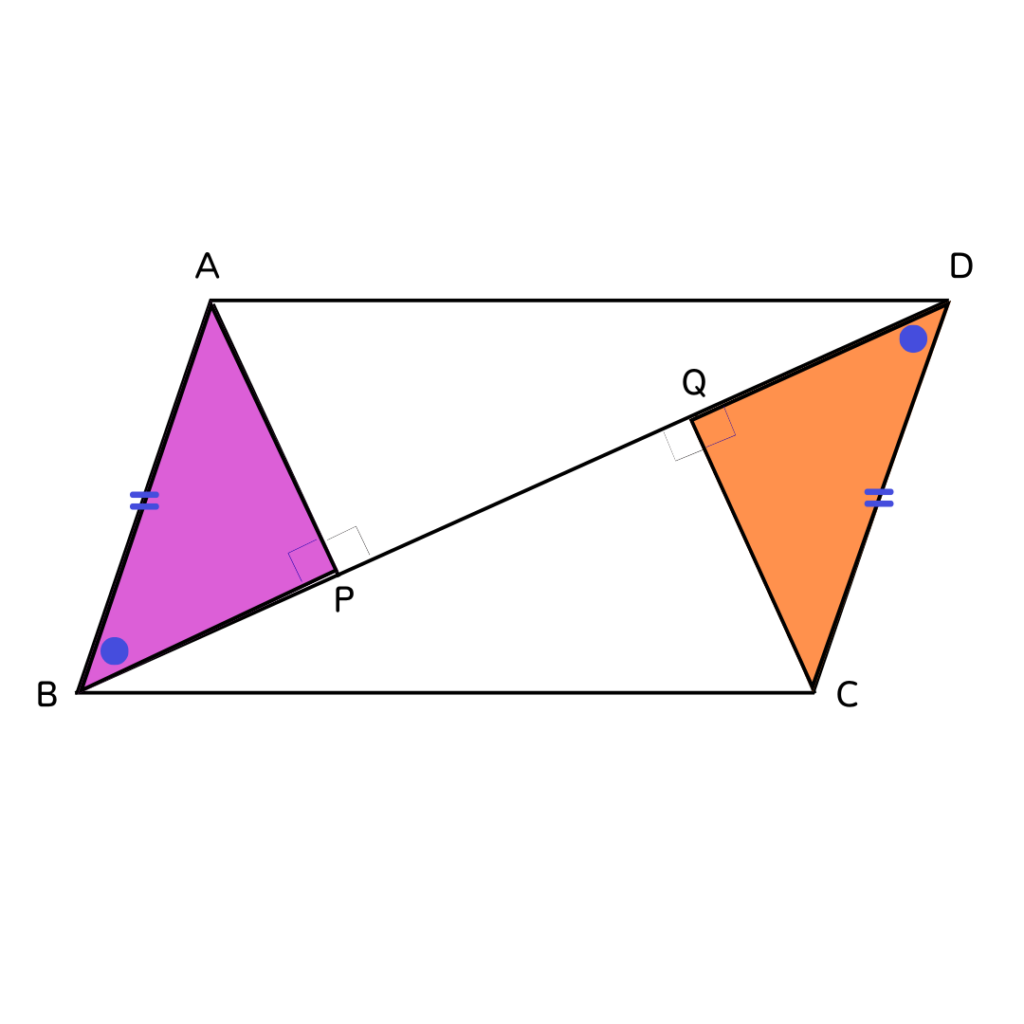
辺(BPとDQ)が等しいのは仮定ではムリだよね…。
なので、対応する鋭角に注目💡
AB∥CDより∠ABPと∠CDQは錯角で
等しくなります✨
よって…
∠ABP=∠CDQ…③
【ステップ3】
これで使う直角三角形の合同条件を書こう❗
①、②、③より
直角三角形の斜辺と一つの鋭角がそれぞれ等しいので
【ステップ4】
2つの三角形の合同を≡(記号)で書こう❗
△APB≡△CQD
【ステップ5】
合同な図形は対応する辺の長さが
それぞれ等しいので
AP=CQ
こんな感じかな✨
答えだけをまとめて書くと…
△APBと△CQDにおいて
平行四辺形ABCDより向かい合う辺が等しいので
AB=CD…①
仮定より ∠APB=∠CQD=90°…②
AB∥CDより錯角は等しいので
∠ABP=∠CDQ…③
①、②、③より
直角三角形の斜辺と一つの鋭角がそれぞれ等しいので
△APB≡△CQD
合同な図形は対応する辺の長さがそれぞれ等しいので
AP=CQ
平行四辺形の性質から、どの三角形の合同を証明するか考えるのが
ポイントだよ✨
三角形だけでなく直角三角形の合同を証明する
パターンあるからそこも覚えておくといいよ👍
📝See an Example Problem2
下の図のように、平行四辺形ABCDの各中点を
それぞれE、F、G、Hとするとき、
四角形EFGHは平行四辺形であることを証明せよ。
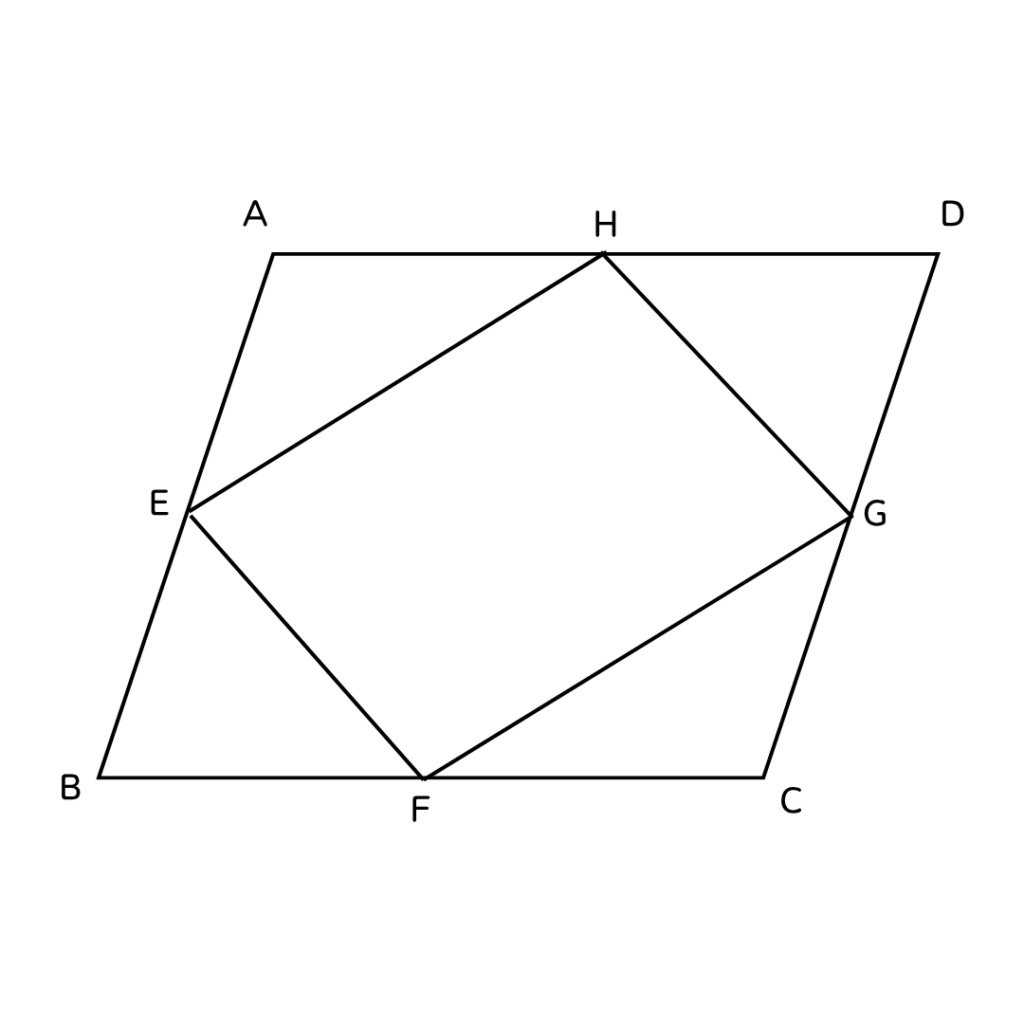
【ポイント✨】
平行四辺形って言いたいときにはこれ❗
平行四辺形になるための条件をここで復習💡
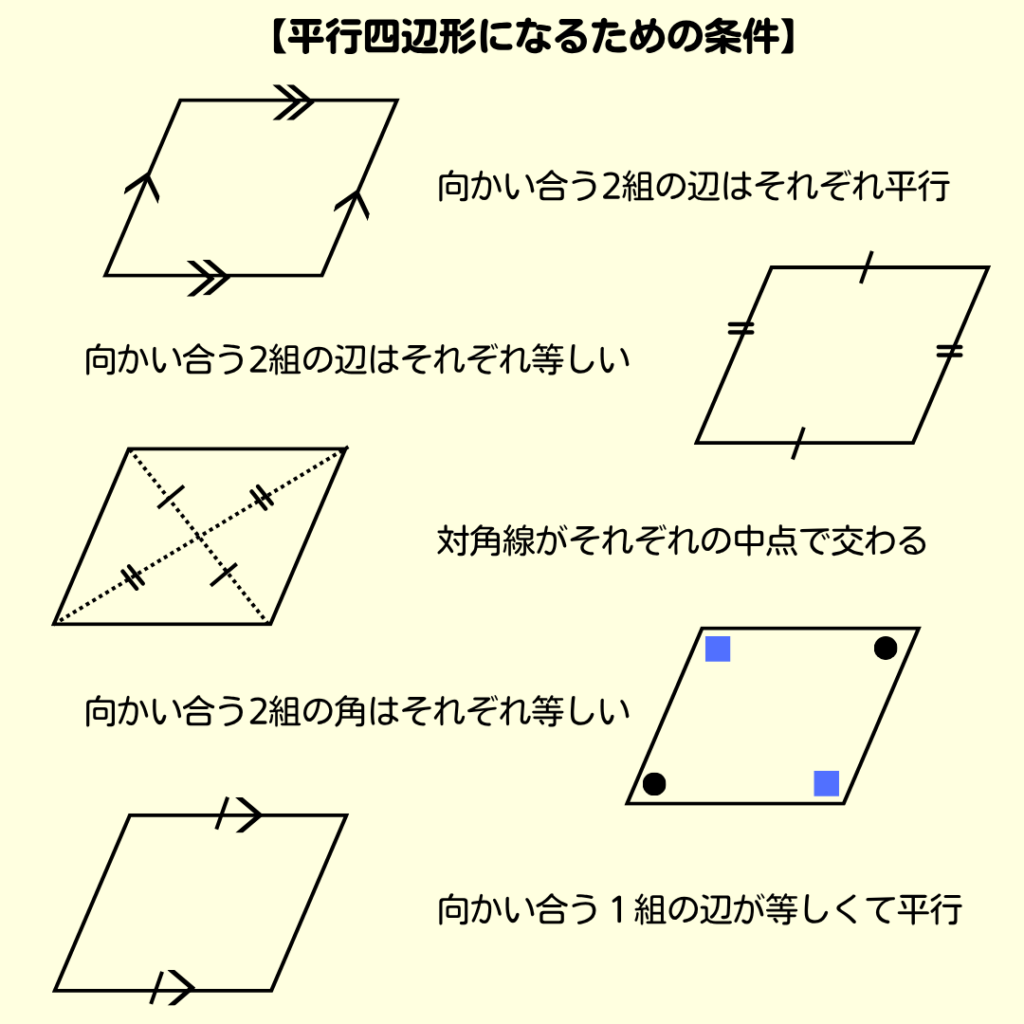
ではでは、進みましょう✍️
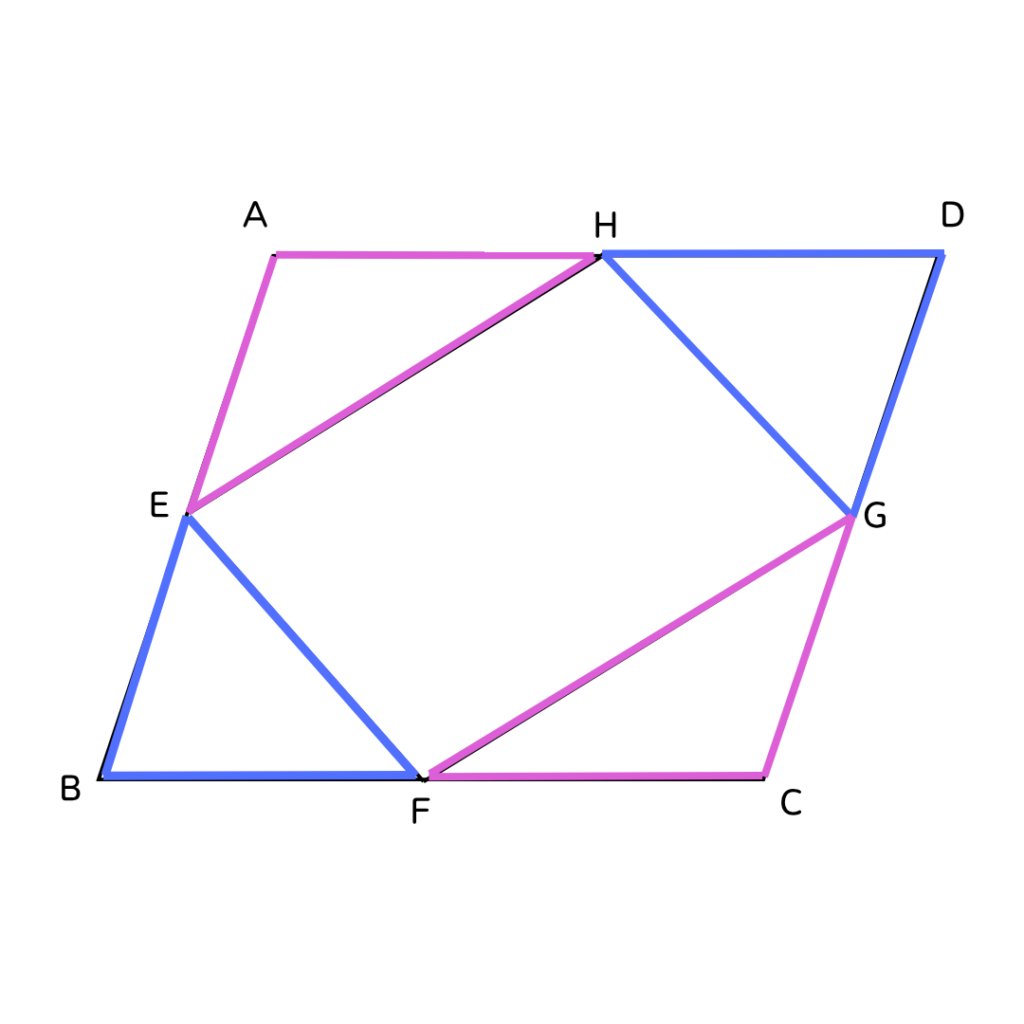
「四角形が平行四辺形になる」が目的☝️
だから、三角形の合同を証明して、平行四辺形に
なるための条件をみたすようにしていこう❗
問題文と平行四辺形の性質から図に同じ長さの辺と
角度を書き込むとこんな感じになるね✨
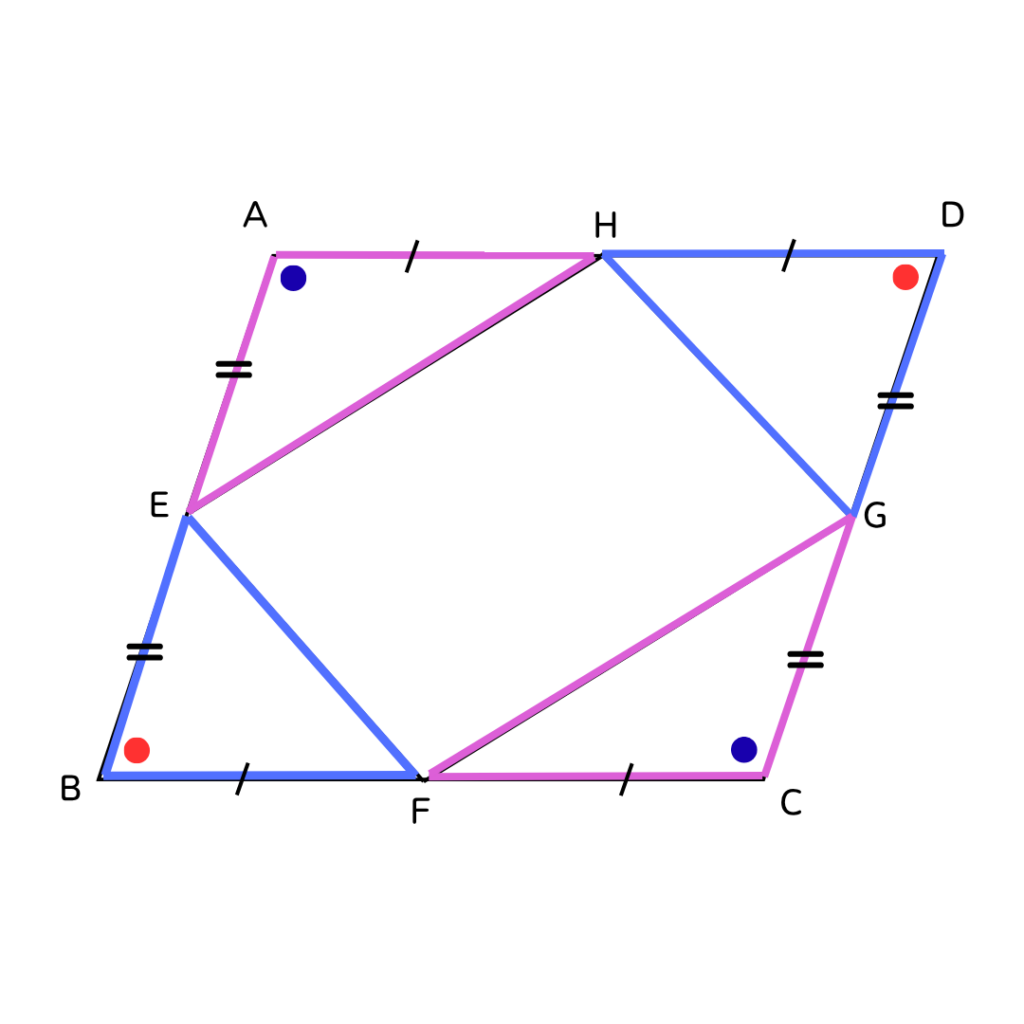
図から考えると…
平行四辺形になるための条件で、
向かい合う2組の辺がそれぞれ等しい
が使えそうな感じ🤔
なので…
△AHEと△CFGと△BFEと△DHG
をそれぞれについて合同って言えればいいよね。
では、この方向で進んでみよう❗
まずは、△AHEと△CFGから🤚
【ステップ1】
△AHEと△CFGにおいて
【ステップ2】
平行四辺形ABCDで
向かい合う角がそれぞれ等しいので
∠HAE=∠FCG…①
平行四辺形ABCDで、向かい合う辺がそれぞれ等しい
また、点E、F、G、Hはそれぞれ中点なので
AE=CG…②
AH=CF…③
【ステップ3】
これで、使う三角形の合同条件を書こう✨
①、②、③より
2組の辺とその間の角がそれぞれ等しいので
【ステップ4】
2つの三角形の合同を≡(記号)で書く💡
△APB≡△CQD
【ステップ5】
合同な図形は対応する辺の長さが
それぞれ等しいので
EH=GF…④
ここでは、辺が等しいってのを最後に平行四辺形に
なるってところで使いたいから番号ふっておくよ。
同じカンジで△BFEと△DHGも進めていくよ😀
【ステップ1】
△BFEと△DHGにおいて
【ステップ2】
平行四辺形ABCDで
向かい合う角がそれぞれ等しいので
∠EBF=∠GDH…⑤
平行四辺形ABCDで、向かい合う辺がそれぞれ等しい
また、点E、F、G、Hはそれぞれ中点なので
EB=GD…⑥
BF=DH…⑦
【ステップ3】
これで、使う三角形の合同条件を書こう✨
⑤、⑥、⑦より
2組の辺とその間の角がそれぞれ等しいので
【ステップ4】
2つの三角形の合同を≡(記号)で書く💡
△BFE≡△DHG
【ステップ5】
合同な図形は対応する辺の長さが
それぞれ等しいので
EF=GH…⑧
これで向かい合う2組の辺がそれぞれ等しいって
いえるから平行四辺形になるって最後に書こう❗
④、⑧より
向かい合う2組の辺がそれぞれ等しいので
四角形EFGHは平行四辺形である。
こんな感じかなっと✨
△AHEと△CFGにおいて
平行四辺形ABCDで
向かい合う角がそれぞれ等しいので
∠HAE=∠FCG…①
平行四辺形ABCDで、向かい合う辺がそれぞれ等しい
また、点E、F、G、Hはそれぞれ中点なので
AE=CG…②
AH=CF…③
①、②、③より
2組の辺とその間の角がそれぞれ等しいので
△APB≡△CQD
合同な図形は対応する辺の長さが
それぞれ等しいので
EH=GF…④
同様に、△BFEと△DHGにおいて
△BFE≡△DHG
合同な図形は対応する辺の長さが
それぞれ等しいので
EF=GH…⑤
④、⑤より
向かい合う2組の辺がそれぞれ等しいので
四角形EFGHは平行四辺形である。
平行四辺形になるための条件は5つあります。
なので最初に図形に仮定などを書き込んで
どの条件を使うのか考えるのがポイントです✨
今回のステップアップゼミ数学は
こんなカンジの問題の類題です💡
【1月のご案内】
次回のステップアップゼミ数学
1月24日(土)開催予定!
【中1の単元】
おうぎ形の弧の長さと面積
中心角の求め方
【中2の単元】
平行四辺形の証明
等積変形
ちょっと理解しにくい単元だね。
ここで一回クリアにしておこう❗
ゼミの授業内容は、ITTO個別指導学院 長野の
ホームページにアップします❗
ITTO長野のホームページでは
学習にまつわるコンテンツを随時更新中🎉
またお目にかかること楽しみにしております✨








