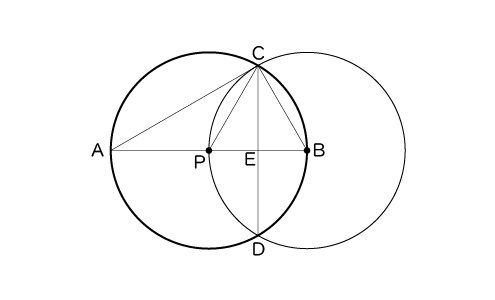令和5年長野県公立高校入試問題 数学問4解説
図形の問題 チャレンジしてみよう!
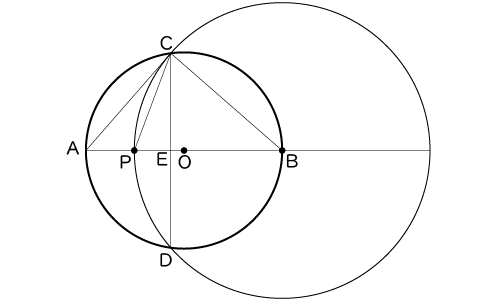
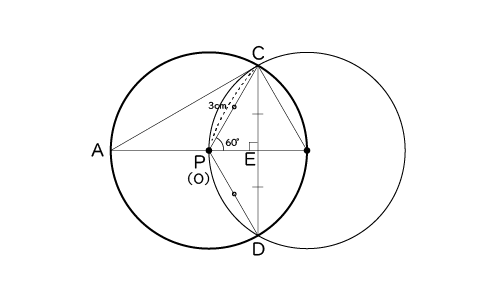
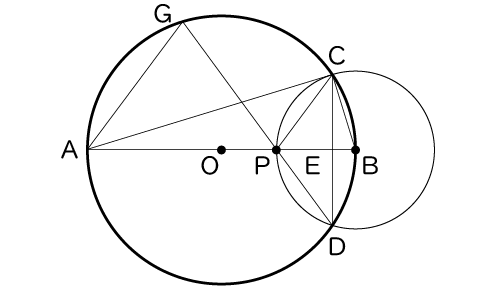
点を動かしたり,図形の大きさを変えたりすることができる数学の作図ソフトがある。桜さんは,その作図ソフトを使って,次の作図の手順に従って図1をかき,点Pを線分AB上で,点Aから点Bの向きに動かしたときの図形を観察した。
〔作図の手順〕
- 長さが6㎝の線分ABを直径とする円Oを書く。
- 線分AB上に点Pをとる。ただし、点Pは点A、Bと重ならないものとする。
- 点Bを中心として、線分BPを半径とする円Bをかく。
- 円Oと円Bの交点をそれぞれC、Dとする。
- 点Cと点Dを結び、線分ABと線分CDの交点をEとする。
- 点Cと3点A、P、Bをそれぞれ結ぶ。
なお,「点Pを線分AB上のどこにとっても、線分ABと線分CDは垂直に交わる。」このことは、(1)~(4)の解答において、証明せずに用いてよい。
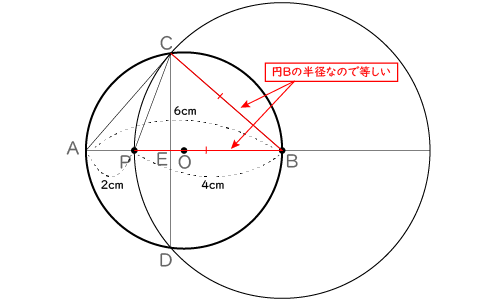
(1) 図1において、点Pを、AP=2cmの位置にとったとき、BCの長さを求めなさい。
(2)1 円Oの半径より、PC=PB
円Bの半径より、BC=PB
よってPC=BC=PBとなるので△PBCは正三角形である。
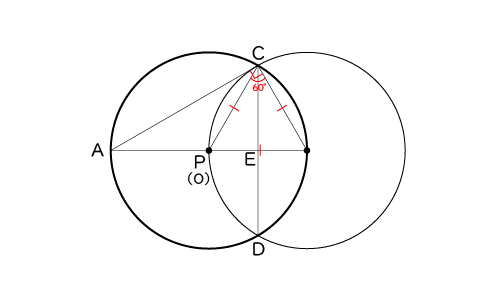
正三角形の1つの内角は60°なので∠PCB=60°
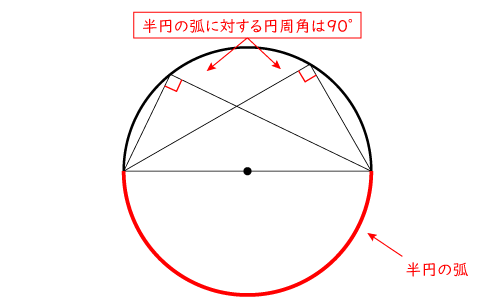
また、∠ACBは円Oの半円の弧に対する円周角なので∠ACB=90°
よって∠ACP=∠ACB-∠PCB=90°-60°=30°
(答)30°
(3)桜さんは、作図ソフトで何度も点Pを線分AB上で動かしているうちに、次の2つのことが成り立つのではないかと予想を立てた。
〔予想〕点Pを線分AB上のどこにとっても、
【1】 △ABCと△CBEは相似である。
【2】 線分CPは∠ACEを二等分する。
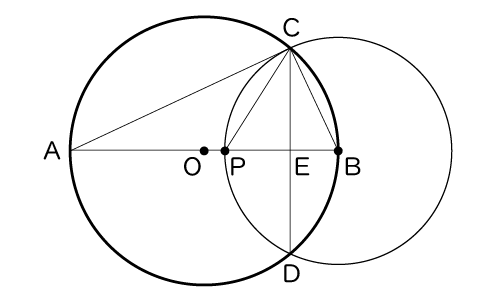
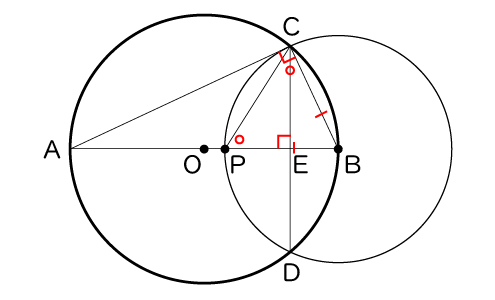
桜さんの予想は、図3を用いて、次のようにそれぞれ証明することができる。
図3
予想【1】の証明
△ABCと△CBEで、『 あ 』だから、∠ACB=90°
AB⊥CDだから、∠CEB=90°
よって、∠ACB=∠CEB …①
『 い 』
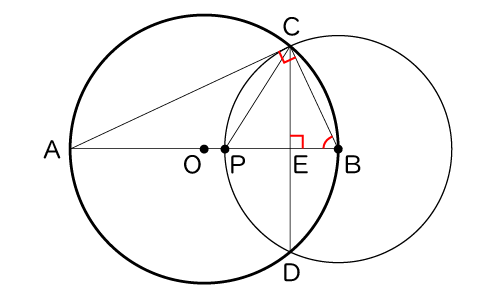
予想【2】の証明
『 あ 』だから、∠ACB=90°
∠ACB=∠ACP+∠PCBより
∠ACP=90°-∠PCB…①
AB⊥CDだから、△CPEは∠CEP=90°の直角三角形であり、
∠CEP=90°-∠CPE…②
『 う 』
よって、∠PCB=∠『 え 』…③
①、②、③より、∠ACP=∠PCE
したがって、線分CPは∠ACEを二等分する。
1)『 あ 』に当てはまる、∠ACB=90°の根拠となることがらを書きなさい。
ただし、予想【1】の証明の『 あ 』と予想【2】の証明の『 あ 』には共通なことがらが入る。
2)『 い 』に証明の続きを書き、予想【1】の証明を完成させなさい。
3) 予想【2】の証明において、『 う 』には③の根拠となることがらを、『 え 』には最も適切な角を記号を用いて、それぞれ書きなさい。
予想【1】の証明
△ABCと△CBEで、『(あ)∠ACBは円Oの半円の弧に対する円周角』だから、∠ACB=90°
AB⊥CDだから、∠CEB=90°
よって、∠ACB=∠CEB …①
『(い)∠ABCは共通な角だから、
∠ABC=∠CBE…②
①、②より、2組の角がそれぞれ等しいので、△ABC∽△CBE』
予想【2】の証明
『(あ)∠ACBは円Oの半円の弧に対する円周角』だから、∠ACB=90°
∠ACB=∠ACP+∠PCBより
∠ACP=90°-∠PCB…①
AB⊥CDだから、△CPEは∠CEP=90°の直角三角形であり、
∠CEP=90°-∠CPE…②
『(う)BCとBPは円Bの半径なので、BC=BPである。
△BCPにおいて、2つの辺が等しいので、△BCPは
二等辺三角形である。』
よって、∠PCB=∠『(え)CPE』…③
①、②、③より、∠ACP=∠PCE
したがって、線分CPは∠ACEを二等分する。
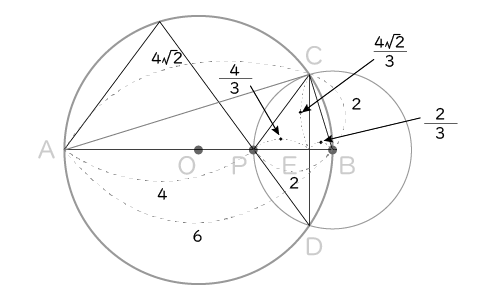
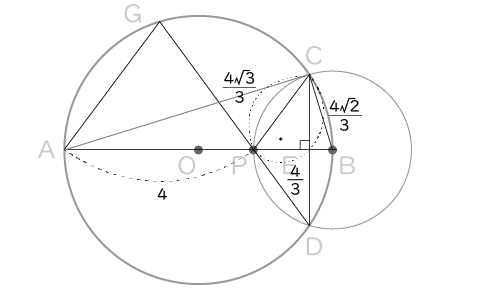
① PB=AB-AP=6-4=2、また円Bの半径よりPB=BC=2
△ACBは∠C=90°の直角三角形なので、三平方の定理よりAC2+BC2=AB2となるから、AC2+22=62を解いてAC=4√2
(3)より△ABC∽△CBEなので、対応する辺の比は等しいから、AC:CE=AB:CBとなる。
よって4√2:CE=6:2を解いて、CE=(4√2)/3
同様に、CB:EB=AB:CBより2:EB=6:2を解いて
EB=2/3,さらにPE=PB-EB=2-2/3=4/3
よって、△CEPの面積は、
PE×CE×1/2=4/3×(4√2)/3×1/2=(8√2)/9
(答) (8√2)/9cm