※受付終了【11月】ステップアップゼミ数学
やっとテストが終わった…

期末は苦手なところだ…
でも点数は上げたい!

やばいな…
次で挽回しないと…
本格的にマズいわ…
そんなとき…
ITTO個別指導学院 長野の
ステップアップゼミがあるよ✨
↓詳しくはこちら↓
数学ステップアップゼミ
11月は
11月22日(土)
開催!
学年なんて関係ない!
中学生なら必要な単元を選んで参加OK!
2つとも参加もできるよ!
🎈川中島校・青木島校🎈
中1の単元 13:00~13:50
中2の単元 14:00~14:50
🪄篠ノ井校🪄
中1の単元 13:00~13:50
中2の単元 16:00~16:50
★お申し込みは11月14日(金)まで!★
📝受講料📝
3,010円(税込み)
11月のステップアップゼミ【数学】
中1の単元
【比例・反比例の利用問題】
中2の単元
【三角形の性質、合同の証明】
授業時間は50分
✨【とってもよくわかる解説(15分くらい)】
🖍️【問題を解く時間もたっぷり(20分くらい)】
🎉【やさしいポイント解説(15分くらい)】
11月【中1の単元】はこんな感じ
📝See an Example Problem1
あります。
これについて以下の問いに答えなさい。
①燃える時間を\(\:x\:\)分、ロウソクが燃えた長さを\(\:y\:cm\)として、\(\:x\:\)を\(\:y\:\)の式で表しなさい。
②このロウソクを13分間燃やしたとき、
ロウソクが燃えた長さは何\(cm\)ですか。
③このロウソクのもとの長さは\(11cm\)です。
このロウソクが半分になるまでの時間は、何分何秒であるか求めなさい。
【ポイント☝️】
\[★比例の関係が成り立ってると…\] \[\:x\:が2倍、3倍になると、\:y\:も2倍、3倍になるよ\]
\[★利用問題は、問題文を表や図に整理することから\] \[始めよう!\]
👉では①から進めていきましょう!

こう見てくと…
\[\:x\:が2倍、3倍になると、\:y\:も2倍、3倍になるよね\]
だから、比例の関係。
つまり、\(\:y=ax\:\)になるから、\(\:x\:が1のときの\:y\:の値をaに入れて\)
\[\large{y=0.4x}\]が答え!
👉この調子で②にいこう
\(【1分間に0.4㎝燃える】\)って書いてあるね
これを13分間燃やすので、燃えた長さは…
\[0.4cm\times13分=5.2cm\]
だから答えは…
\[\large{5.2㎝}\]
だよ!
👉最後に③
\[11cm\div2=5.5cm\]だね。
だから、ロウソクが燃えた長さも\(\:\large{5.5㎝}\:\)だよね。
次に、1分間に\(0.4cm\)燃えるので何分かかるかは…
\[5.5cm\div0.4cm=13.75分\]って分かるよ✨
問題文は【何分何秒ですか。】って聞いてるので
13.75分だと解答としては間違い…
だから、\(\mathbf{13.75分を13分+0.75分}\)って考えよう💡
そうすると、0.75分が何秒か考えればいいね
分→秒にするには60をかけてあげればいいよ👍
なので…
\[0.75\times60=45秒\]
だから… \[\large{13分45秒}\] これが答え!
☝️③のもう一つの考え方
ロウソクの燃えた長さが\(5.5cm\)なわけなので、
\(\:y=0.4x\:\)の\(\:y\:\)に5.5を代入する。
\[\:5.5=0.4x\]
左辺と右辺を入れ替えて
\[\:0.4x=5.5\]
両辺を10倍して
\[\:4x=55\]
両辺を4でわって
\[\frac{4}{4}x=\frac{55}{4}\]
\[\:x=13.75\]
って感じ✨
あとはさっきと同じ解き方で答えまで
もっていきましょう!
こっちのほうが比例の考え方を
使ってる感じはあるけど…。
分かりやすいほう・ミスない方で解けるといいよね👍
📝See an Example Problem2
\(その面積は20㎠です。\)
①\(\:x\:,\:y\:を使って\:y\:を\:x\:の式で表しなさい。\)
\(また、式は比例、反比例のどちらですか。\)
②\(\:x\:,\:y\:がともに整数のとき、\)
\((\:x\:,\:y\:)の組み合わせをすべて答えなさい。\)
【ポイント✌️】
\[★\:y=\frac{a}{x}は変形すると\:xy=a\:だよ\] \[だから反比例だったらどちらかの形になるはず💡\] \[ただ、式で表しなさいってときは、\:y=\frac{a}{x}で書こう📝\] \[ここはそういう決まりだって思ってね\]
\[★反比例の関係が成り立ってると…\] \[\:x\:が2倍、3倍になると、\:y\:は\frac{1}{2}倍、\frac{1}{3}倍になるよ\]
\[★利用問題は、問題文を表や図に整理することから\] \[始めよう!\]
👉まず①から
\(だから、問題通りに式を作ると…\)
\[\:xy=20\]ってなるよ✍️
\(これを見たら反比例って分かっちゃう🎉\)
\(さらに【ポイント✌️】から、\)\[\:y=\frac{20}{x}\]\(ってできるね♪\)
もうこれで答えだよ👍
まとめると…
\[式:\:y=\dfrac{20}{x}、\mathbf{反比例}\]
だね。
👉では②
簡単に言うと
【2つの整数をかけ算して20になる組み合わせ】
ってこと✨
ここで\(\:x\:と\:y\:\)はなんだったかを確認しましょう
長方形の縦の長さと横の長さなので、負の整数ではないはずです!
つまり…
【2つの正の整数】で【かけ算すると20になる】
組み合わせを考えよう🫵
数えてるときに抜けがあるといけないので、
表を作ってみよう✨
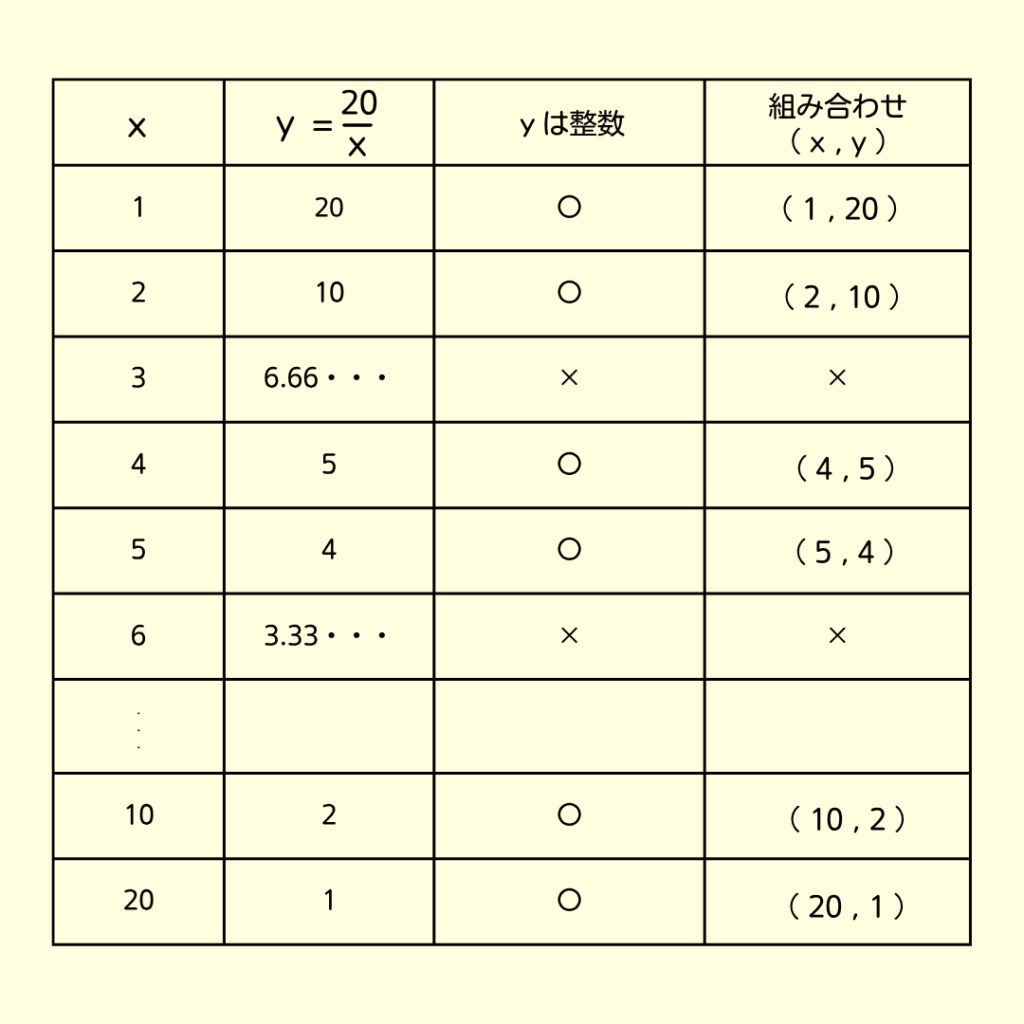
なので、答えは…
\((1,20)(2,10)(4,5)(5,4)(10,2)(20,1)の6通り\)
だね👍
比例・反比例は表にしてみよう📝
そうすると、数字がどう変わってるのか
実際に見えるよ💡
これで、グッとわかりやすくなるよ✨
11月【中2の単元】はこんな感じ
📝See an Example Problem1
【ポイント☝️】
\[【三角形の合同条件】\] \[・3組の辺がそれぞれ等しい\] \[・2組の辺とその間の角がそれぞれ等しい\] \[・1組の辺とその両端の角がそれぞれ等しい\]
\[これは確実にメモライズ(記憶)しておきましょう💡\]
【ポイント✌️】
\[★証明の手順★\] \[\large{【はじめ】}\] \[証明する2つの三角形を書こう\]
\[\large【なか】\] \[問題文と図から等しい辺や角を書こう\]
\[\large【おわり】\] \[なかの条件に会う合同条件を書く\] \[2つの三角形の合同を記号で示す\]
\[\large【辺の長さや角度が同じことを証明したいとき】\] \[合同な図形は対応する辺または角がそれぞれ等しいので\] \[と書いてから同じ辺や角度を書く\]
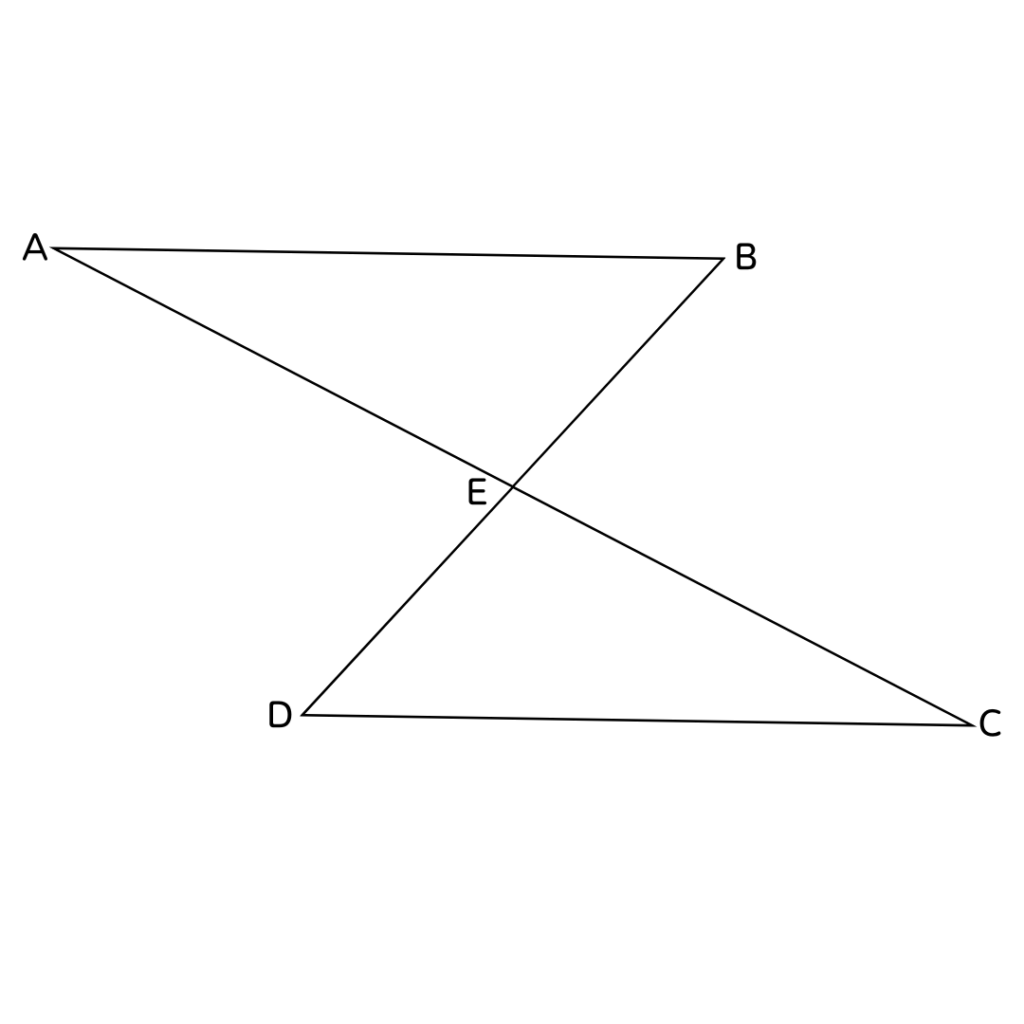
👉では、この問題の証明をしていこう
\(AB=CD、AB//DCを書き込む\)
今回は問題文に合同な三角形になるものが
書いてあるからそれを書く✍️
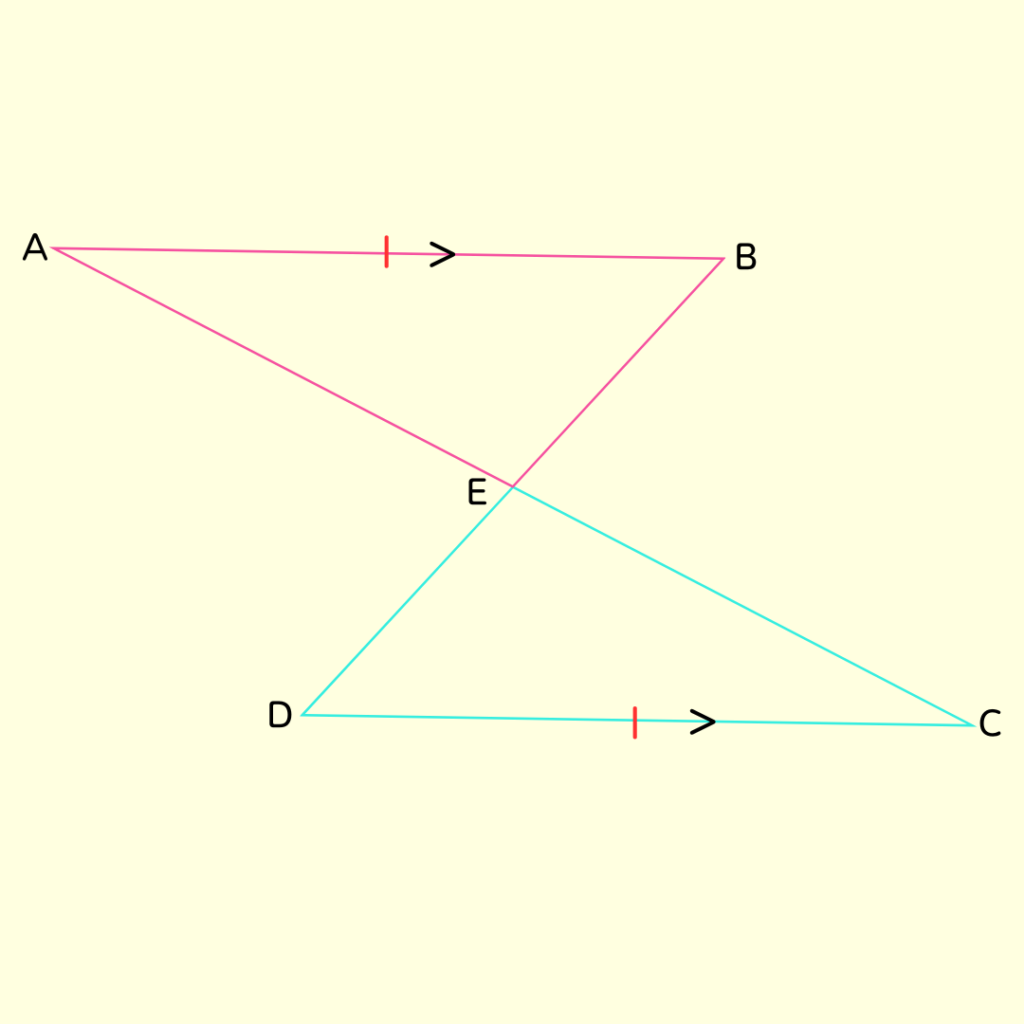
\[△EABと△ECDにおいて\] それじゃ【なか】
合同条件には辺の長さか角の大きさしかない💡
問題文に等しい辺があるから、
これは根拠として使えるよ👍
問題文に書いてあるものの理由は仮定でいいからね
\[仮定より、AB=CD・・・①\] ひとつ目の根拠として番号をつけておくよ
もうひとつ問題文に\(\:AB//DC\:\)があるけど…
これは平行だけなので合同条件の根拠にはならない❌
平行線があったら、同位角・錯角が等しくなるっていうのを思い出して❗
そうすると角の大きさの根拠が出てくるはず♪
これを図に書き込む✍️と…
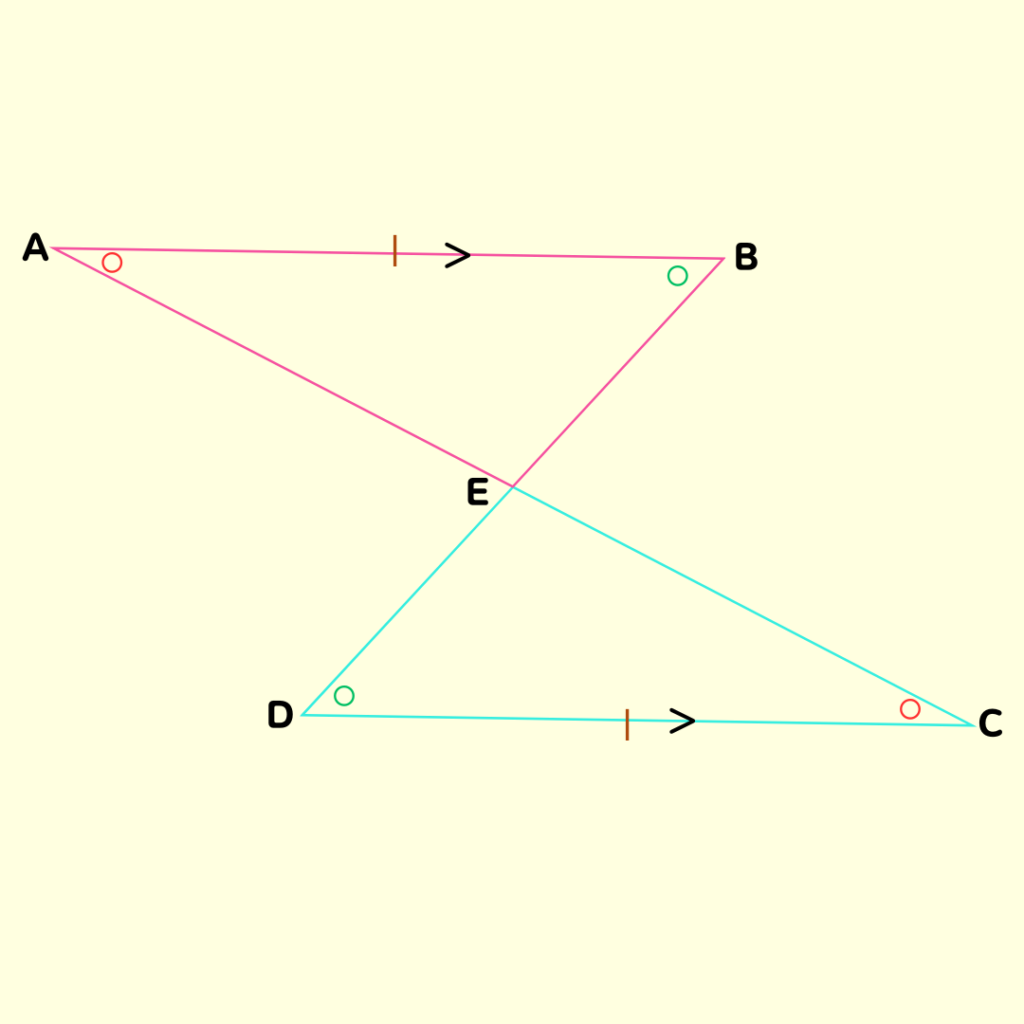
この図形だと錯角が使えるね🗝️
これを書く
\[AB//DCより、錯角が等しいので\] \[∠ABE=∠CDE・・・②\] \[∠BAE=∠DCE・・・③\] これで角の大きさの根拠が2つできた✨
最後に【おわり】だね。
\[①、②、③より\] \[1組の辺とその両端の角がそれぞれ等しいので\] \[△EAB≡△ECD\] これでカンペキ🎉
まとめておこう!
\[△EABと△ECDにおいて\] \[仮定より、AB=CD・・・①\] \[AB//DCより、錯角が等しいので\] \[∠ABE=∠CDE・・・②\] \[∠BAE=∠DCE・・・③\] \[①、②、③より\] \[1組の辺とその両端の角がそれぞれ等しいので\] \[△EAB≡△ECD\]
証明問題は…
最初は模範解答まねして書いていくと慣れてくるよ!
証明書き始める前に
図を見ながら、どの合同条件になるのか
見つけられるかがポイントになるからね👍
📝See an Example Problem2
このとき、∠CGB=∠CEDであることを証明しなさい。
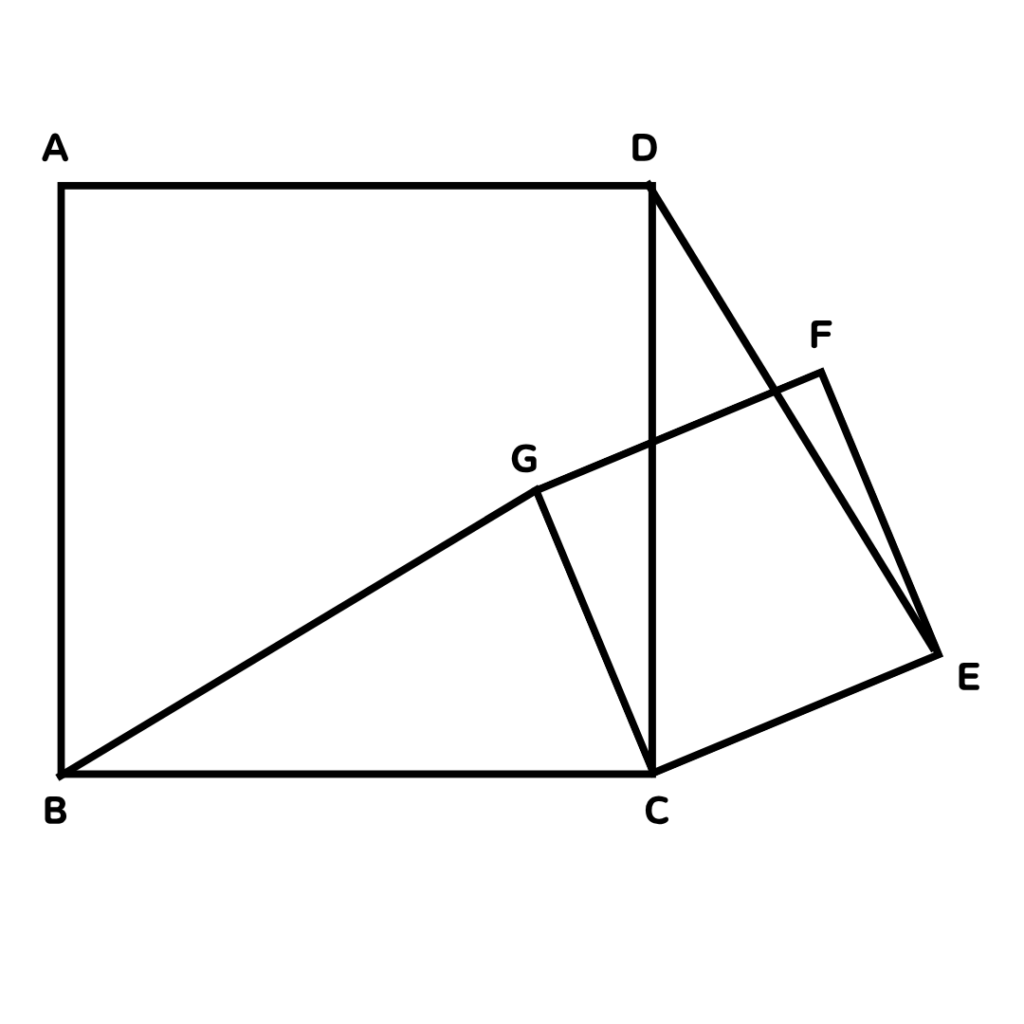
この問題は、2つの三角形が合同だから
合同な三角形の角は等しいよ
って証明したい問題。
だから、まず合同って言いたい2つの三角形の発見から。
では進めてみよう!
問題文に正方形が2つあるので、
辺の長さが等しいところと
証明したい角の大きさ(★)で書き込んでみたよ💡

これを見ると、証明したい2つの三角形が分かるね👍
★のある2つの三角形の合同を証明すればいいね
なので【はじめ】は…
\[△CBGと△CDEにおいて\] になるね。
図を見れば【なか】も2つはいけるはず💡
2組の辺がそれぞれ等しいことが分かるよね
\[正方形ABCDなので、BC=DC・・・①\] \[正方形CEFGなので、CG=CE・・・②\] ここまでは進められる。
で、あとは…
2辺の間の角が等しいって言えればいいけど…
ここはちょっとむずい…
なのでちょっとした図を見てみよう💡
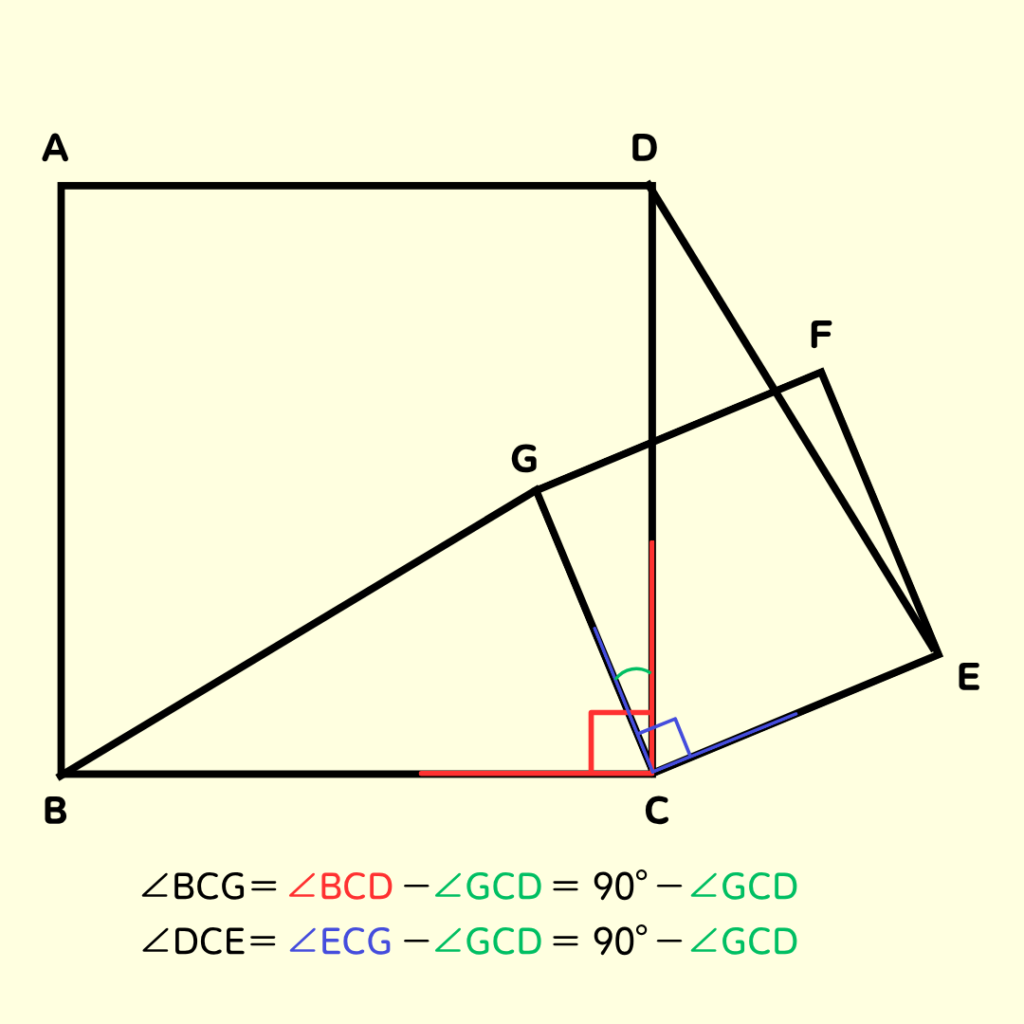
それぞれから∠GDCをひくと…
∠BCGと∠DCEになる
同じものから同じものをひいたものは同じもの❗ってことで…
∠BCG=∠DCEとなるってこと❗
これを証明の書き方にすると… \[∠BCG=∠BCD-∠GCD=90°-∠GCD・・・③\] \[∠DCE=∠ECG-∠GCD=90°-∠GCD・・・④\] \[③、④より\] \[∠BCG=∠DCE・・・⑤\] ここまで来たらもう少し📝
ここから【おわり】
\[①、②、⑤より\] \[2組の辺とその間の角がそれぞれ等しいので\] \[△CBG≡△CDE\] で、【辺の長さや角度が同じことを証明したいとき】の
\[合同な図形の対応する角の大きさは等しいので\] \[∠CGB=∠CED\] 長かった…💦
解答をまとめよう!
\[△CBGと△CDEにおいて\] \[正方形ABCDなので、BC=DC・・・①\] \[正方形CEFGなので、CG=CE・・・②\] \[また\] \[∠BCG=∠BCD-∠GCD=90°-∠GCD・・・③\] \[∠DCE=∠ECG-∠GCD=90°-∠GCD・・・④\] \[③、④より\] \[∠BCG=∠DCE・・・⑤\] \[①、②、⑤より\] \[2組の辺とその間の角がそれぞれ等しいので\] \[△CBG≡△CDE\] \[合同な図形の対応する角の大きさは等しいので\] \[∠CGB=∠CED\]
角の大きさが等しいって言いたいときに、
同じものから同じものをひいたものは同じもの❗
これを使うことが多いので、できるようにしておけば
なおOKかな👍
今回のステップアップゼミ数学は
こんなカンジの問題の類題です💡
【12月のご案内】
次回のステップアップゼミ数学
12月27日(土)開催予定!
【中1の単元】
平面図形・作図
【中2の単元】
平行四辺形の性質
平行四辺形になるための条件
ゼミの授業内容は、ITTO個別指導学院 長野の
ホームページにアップします!
ITTO長野のホームページでは
学習にまつわるコンテンツを随時更新中🎉
またお目にかかること楽しみにしております✨








