※受付終了【1月】ステップアップゼミ数学
いよいよ3学期

今のうちにわからない問題を解決しておきたい🙌

2学期期末テストで思うような結果じゃなかった💦
そんなとき…
ITTO個別指導学院 長野の
ステップアップゼミがあるよ✨
↓詳しくはこちら↓
数学ステップアップゼミ
1月は
1月24日(土)
開催!
学年なんて関係ない!
中学生なら必要な単元を選んで参加OK👍
2つとも参加もできるよ✨
🎈川中島校・青木島校🎈
中1の単元 13:00~13:50
中2の単元 14:00~14:50
🪄篠ノ井校🪄
中1の単元 13:00~13:50
中2の単元 16:00~16:50
★お申し込みは1月16日(金)まで!★
📝受講料📝
3,010円(税込み)
1月のステップアップゼミ【数学】
中1の単元
【おうぎ形の弧の長さと面積】
【おうぎ形の中心角の求め方】
中2の単元
【平行四辺形の性質を使った証明】
【面積が同じ図形の問題】
授業時間は50分
✨【とってもよくわかる解説(15分くらい)】
🖍️【問題を解く時間もたっぷり(20分くらい)】
🎉【やさしいポイント解説(15分くらい)】
1月【中1の単元】は
こんな感じの問題
📝See an Example Problem1
下の図のおうぎ形の弧の長さと面積を求めなさい。

【✨ポイント✨】
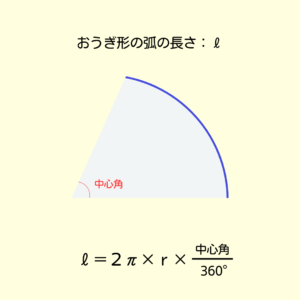
おうぎ形の弧の長さと面積を求める公式
→これを知らないと解けないよ💡
rは半径の長さです。
では、解いていこう👍
まずは弧の長さ💡
半径が3㎝で中心角は40°が図から分かるね✨
弧の長さの公式は・・・\[2\times π\times r\times \frac{中心角}{360}\] だから、\(rに3、中心角に40を入れるよ\)
\[2\times π\times 3\times \bbox[orange,4px]{\frac{40}{360}}\] 約分して… \[2\times π\times \bbox[lightgreen,4px]{3\times \frac{1}{9}}\] 先に緑の部分を計算して \[2\times π\times \frac{1}{3}\] よって \[\frac{2}{3}π\] 答えは \[\mathbf{\frac{2}{3}π cm}\]
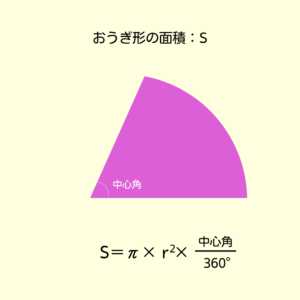
次に面積だね💡
半径が3㎝で中心角が40°は変わらないから
面積の公式は…\[π\times r^2\times \frac{中心角}{360}\] だから、\(rに3、中心角に40を入れるよ\)
\[π\times3^2\times \bbox[orange,4px]{\frac{40}{360}}\] 累乗の計算と約分して… \[π\times 9\times \frac{1}{9}\] よって \[π\] 答えは \[\mathbf{π ㎠}\]
ここは公式知らないとできないから💦
何回も繰り返して公式を覚えてしまいましょう✨
📝See an Example Problem2
下の図のような円錐を展開した際にできる側面積のおうぎ形の中心角を求めなさい。
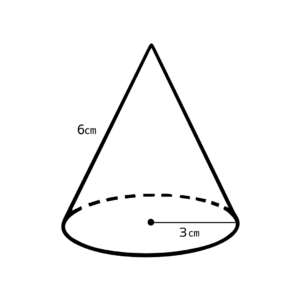
【✨ポイント✨】
円錐の側面のおうぎ形の中心角は簡単❗
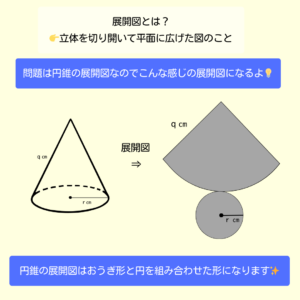
底面の円の円周の長さと側面のおうぎ形の弧の長さが
同じことを利用すると…
下のような式ができるよ💡
✨円錐の側面のおうぎ形の中心角を求める式✨
\[360°\times \frac{底面の円の半径}{円錐の母線の長さ}\]ではやってみよう✍️
問題では…
母線の長さは6㎝、底面の円の半径は3㎝だから💡
1月【中2の単元】は
こんな感じの問題
📝See an Example Problem1
下の図のように、平行四辺形ABCDの対角線の交点Oを通る直線と辺ADと辺BCとの交点をそれぞれE、Fとする。
このとき、AE=FCであることを証明しなさい。
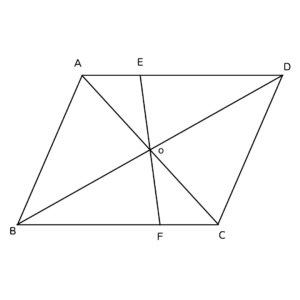
【✨ポイント✨】
平行四辺形の性質と証明の進め方の確認💡
確認はこちらから
この知識はよく使うからね💡
覚えてない子もけっこういるから差がつくよ👍
では進めよう❗
証明したいのはAE=FCだよ。
この辺を含む三角形の【△AEOと△CFO】の合同を証明すればよさそうだね✨
👇図に書き込むとこうだね
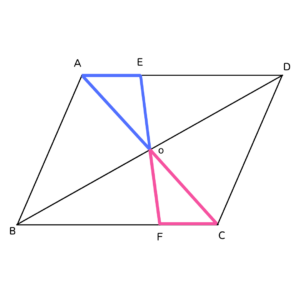
【等しい辺や角は平行線の錯角や平行四辺形の性質から見つけてみよう✨】
AD//BCなので、錯角はそれぞれ等しいから
∠EAO=∠FCO…①
平行四辺形の対角線は中点で交わるから
AO=CO…②
対頂角なので
∠AOE=∠COF…③
【ここで合同条件を書く❗】
①、②、③より
一組の辺とその両端の角がそれぞれ等しいので
△AEO≡△CFO
【結論で言いたいのは、AE=AFなので】
合同な図形の対応する辺の長さは等しいので
AE=FC
こんな感じかな。
模範解答をまとめると…
△AEOと△CFOにおいて
AD//BCなので、錯角はそれぞれ等しいから
∠EAO=∠FCO…①
平行四辺形の対角線は中点で交わるから
AO=CO…②
対頂角なので
∠AOE=∠COF…③
①、②、③より
一組の辺とその両端の角がそれぞれ等しいので
△AEO≡△CFO
合同な図形の対応する辺の長さは等しいので
AE=FC
これでOK❗
証明は何度も繰り返すこと✨
そうすることで…
書き方や等しいものの見つけ方が分かるよ❗
📝See an Example Problem2
下の図で、四角形ABCDはAD∥BCの台形で、Oは対角線AC,BDの交点である。
このとき、次のア~エの三角形の組みのうち、面積が等しいものをすべて選びなさい。
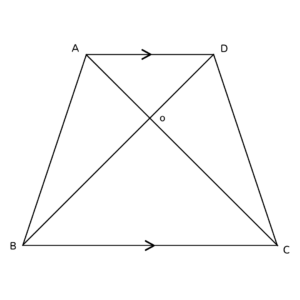
ア △ABDと△ACD
イ △ABCと△ACD
ウ △AODと△BOC
エ △AOBと△DOC
【✨ポイント✨】
等積変形(違う形の図形だけど、面積が等しい2つの図形)の問題。
三角形の形を変化させることが多いかな😀
緑とオレンジの三角形で見てみよう👇

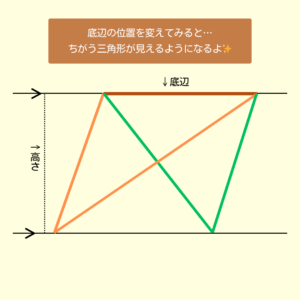
👇同じカンジで青とピンクの三角形も同じ面積になる
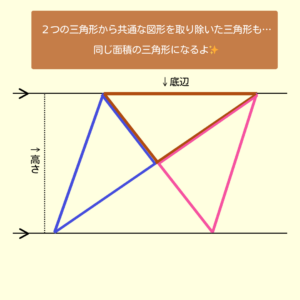
さて、これを踏まえて進めてみましょう✍️
まずは、辺ADを底辺として
高さが同じ三角形を考えてみよう💡
そうすると…
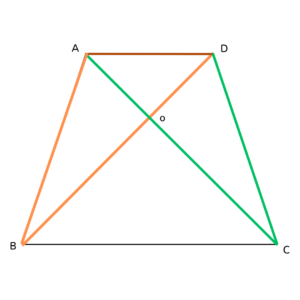
△ABDと△ACDの面積が等しくなりそう✨
だから答えの一つ目は ア だね。
底辺はそのままでもう一組同じ面積の三角形が見えるはず…
ここはさっきのポイントの下のほうだね
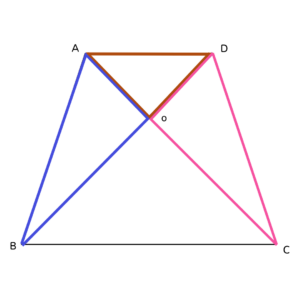
△ABDと△ACDの面積は等しいのはさっき確認したよね。
共通な図形の△AODをそれぞれから取り除いた図形の面積も等しくなるはず。
だから…
△AOB(青)と△DOC(ピンク)は等しいから
もう一つの答えは エ だね。
よって答えは…
アとエになるよ❗
今回はこんな感じのゼミ内容です👆
【2月のご案内】
次回のステップアップゼミ数学
2月21日(土)開催予定
【中1の単元】
空間図形(表面積・体積)
【中2の単元】
場合の数・確率
学校だとさらっといっちゃう単元だね。
もう一度しっかり学んでおこう❗
ゼミの授業内容は、ITTO個別指導学院 長野の
ホームページにアップします❗
ITTO長野のホームページでは
学習にまつわるコンテンツを随時更新中🎉
またお目にかかること楽しみにしております✨







