【8月】ステップアップゼミ数学

2025年７月夏休みスタート！

前学期の数学テスト…思い出してみてください。
いいこと、よくないこと、思うことありますよね。

中２生さん

数学ってけっこうめんどくさいから
「宿題、答えを見ながらやっちゃった…」

中１生さん

先生に覚えなさいって言われたから
「公式は覚えたけど、使い方が…」

そんなモヤモヤ…。
ITTO個別指導学院 長野の数学ステップゼミなら、
解決していけるかも✨

↓詳しくはこちら↓
数学ステップアップゼミ

８月は８月23日（土）開催！

学年なんて関係ない！
中学生なら必要な単元を選んで参加OK！
2つとも参加もできるよ！

🎈青木島校・川中島校🎈
中１の単元　15：00～15：50
中２の単元　16：00～16：50

🪄篠ノ井校🪄
中１の単元　13：00～13：50
中２の単元　16：00～16：50

お申し込み・お問い合わせはこちらから
お申し込みは８月12日（土）までです

８月のゼミの内容はこちら

中1の単元
【方程式の解き方（分数、小数）】

中2の単元
【1次関数（グラフ・方程式）】

授業時間は50分
✨【とってもよくわかる解説（15分くらい）】
🖍️【問題を解く時間もたっぷり（20分くらい）】
🎉【やさしいポイント解説（15分くらい）】

中1の単元はこんな感じの問題

📝See an Example Problem【１】

\[\dfrac{2x+1}{5}=\dfrac{x-7}{4}\]

分数で分子（上の数字）がたし算・ひき算に
なってるときはかっこ()をつけよう！
これだけでミスが減るよ。

\[\dfrac{(2x+1)}{5}=\dfrac{(x-7)}{4}\]

次に、分数っていやだよね…。
分数じゃなくしたい！

☝️ポイント１
問題は、方程式なので、＝の右と左、
両方に同じ数をかけても
\(x\)の値は変わらないよ。（等式の性質）

✌️ポイント２
で、分数をなくすために、ここで最小公倍数をかけるってよく言われるよね。
これがよく分からないって…。
こう言われること多し。
だから、分母（下の数）のかけ算した数字を
両方にかけるといいよ。

これで、問題みてみよう。
\[\dfrac{(2x+1)}{5}=\dfrac{(x-7)}{4}\] だから、\(左は5、右は4なので、5\times4=20\)
ってことで20をそれぞれにかけるよ。
\[\bbox[pink,4px]{20\times}\dfrac{(2x+1)}{5}=\bbox[pink,4px]{20\times}\dfrac{(x-7)}{4}\]

ここで約分しよう！
\[\bbox[pink,4px]{4\times}(2x+1)=\bbox[pink,4px]{5\times}(x-7)\]

文字式のきまりに従うと
\[4(2x+1)=5(x-7)\]

それぞれ()のなかのものにかけて（分配法則）
かっこをはずすと
\[8x+4=5x-35\]

文字を＝の左、数字を＝の右に移動するよ。
（移項だね）
=をまたぐときは符号が変わることに
めっちゃ注意してね。
\[8x\bbox[wheat,4px]{+4}=\bbox[springgreen,4px]{5x}-35\] \[8x\bbox[springgreen,4px]{-5x}=-35\bbox[wheat,4px]{-4}\]

あとは計算！
\[3x=-39\]

\(xの前は3。逆数の\frac{1}{3}をかけるとxだけになるよ。\)
\[\bbox[orange,4px]{\frac{1}{3}\times}3x=\bbox[orange,4px]{\frac{1}{3}\times}(-39)\]
\[\large{x=-13}\]

📝See an Example Problem【２】

\[0.32x+0.14=0.07x+0.64\]
☝️ポイント１
問題は、方程式なので、＝の右と左、
両方に同じ数をかけても
\(x\)の値は変わらないよ。
（等式の性質）

✌️ポイント２
で、小数をなくすために、10倍もしくは
100倍しなさいって言われるよね。
小数点の右側に数字が１個（小数第一位）のみ→10倍
小数点の右側に数字が２個（小数第二位）もある→100倍
両方あるものは必ず全部を100倍しよう。
これは10倍。こっちは100倍とかしないこと！

これで、問題みてみよう。
\[0.32x+0.14=0.07x+0.64\]
これは、小数点の右側に数字が２つあるよね。
ってことでそれぞれを100倍する。
\[\bbox[pink,4px]{100\times}0.32+\bbox[pink,4px]{100\times}0.14=\bbox[pink,4px]{100\times}0.07x+\bbox[pink,4px]{100\times}0.64\]

ここで計算しよう。
\[32x+14=7x+64\]

文字を＝の左、数字を＝の右に移動するよ。
（移項だね）
=をまたぐときは符号が変わることに
めっちゃ注意してね。
\[32x\bbox[wheat,4px]{+14}=\bbox[springgreen,4px]{7x}+64\] \[32x\bbox[springgreen,4px]{-7x}=64\bbox[wheat,4px]{-14}\]

あとは計算！
\[25x=50\]

\(xの前は25。逆数の\frac{1}{25}をかけるとxが出るよ！\)
\[\bbox[orange,4px]{\frac{1}{25}\times}25x=\bbox[orange,4px]{\frac{1}{25}\times}50\]
\[\large{x=2}\]

中2の単元はこんな感じの問題

❗まずは、一次関数とは？ってところ。

関数って基本的には
\(\bbox[pink,4px]{xに数字を入れるとyの数字もひとつに決まる}\)
ってこと。

一次関数だと\(xとyは\)\[\bbox[lightgreen,4px]{y=ax+b}\]で表せます。

たとえば…
消しゴム1個150円と、鉛筆1本100円を
文房具屋さんで買うとします。
鉛筆を何本買ったかを\(x本\)、全部でかかるお金を\(y円\)とすると、
\[\bbox[lightgreen,4px]{y = 100x + 150}\] という式になります。

これは\(\bbox[pink,4px]{xを決めるとyがひとつに決まる}\)ので
一次関数

実は、日常の「買い物」や「料金計算」でも
一次関数が使われているよ！
\(🗝️【y = ax + bの一次関数からわかること】\)

①\( a\)（傾き）…変化の割合を表す
\(\bbox[lightgreen,4px]{変化の割合 ＝(y\;の増加量)÷(x\;の増加量)}\)

たとえば…
\(y = 3x + 2 の場合、傾きは3\)
\(これはxが1増えると、yは3増えるということ。\)
\(つまり、xが3増えれば、yは9増えるよ。\)
この増えたものがそれぞれの増加量です！

👉 変化の割合はいつでも一定。
それが一次関数の特徴です。

② \(b\)（切片）…\(\:\:y\:軸との交点を表します\)
\(bの値は、x = 0 のときの y の値 \)
\(つまり、グラフが通る y\:軸上の点\:(0, b)\:のこと。\)

例：\(y = 3x + 2 の切片は 2\)
👉 グラフは点 （0, 2）を通るよ。

③ 座標を求めてグラフがかける！
\(y = ax + b の式がある。\)
\(→好きな x を代入して、y の値を求めれるよ。\)

例：\(y = 3x + 2\)
\(* x = 1 ⇒ y = 3×1 + 2 = 5 ⇒ 点 (1, 5)\)
\(* x = -1 ⇒ y = 3×(-1) + 2 = -1 ⇒ 点 (-1, -1)\)

👉 こうしていくつか点を出せば、
グラフも簡単にかけます！

📝See an Example Problem【1】

次の一次関数で、表を完成し、グラフをかきなさい。

 \(\large y=\dfrac{1}{3}x-2\)
表を完成させるには…
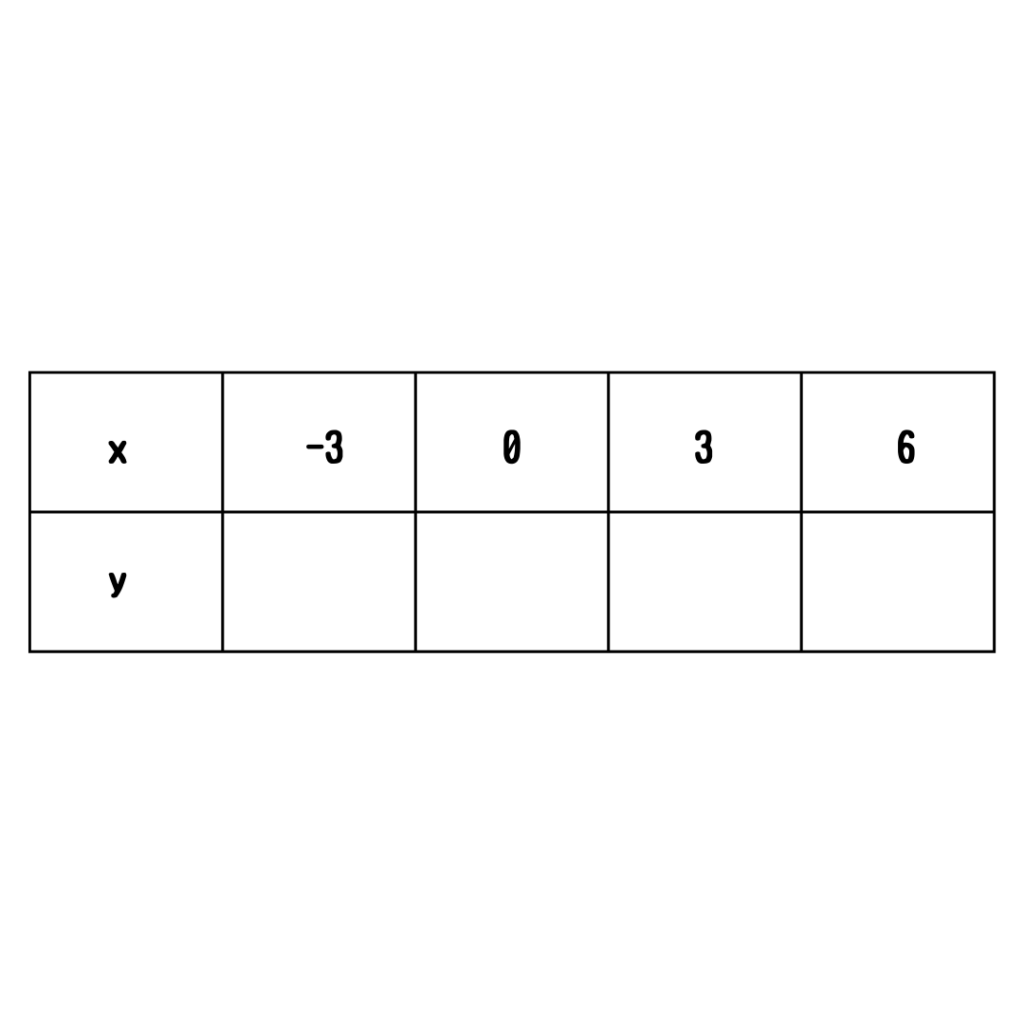
表にある\(x\)の値を式に入れてみよう！

\(x=-3\)のとき
\(y=\dfrac{1}{3}\times(-3)-2=-1-2=-3\)
よって
 \(y=-3\)

\(x=0\)のとき
\(y=\dfrac{1}{3}\times0-2=0-2=-2\)
よって
 \(y=-2\)

\(x=3\)のとき
\(y=\dfrac{1}{3}\times3-2=1-2=-1\)
よって
 \(y=-1\)

\(x=6\)のとき
\(y=\dfrac{1}{3}\times6-2=2-2=0\)
よって
 \(y=0\)

いま計算したものを表に書き込めば完成！
次はグラフ
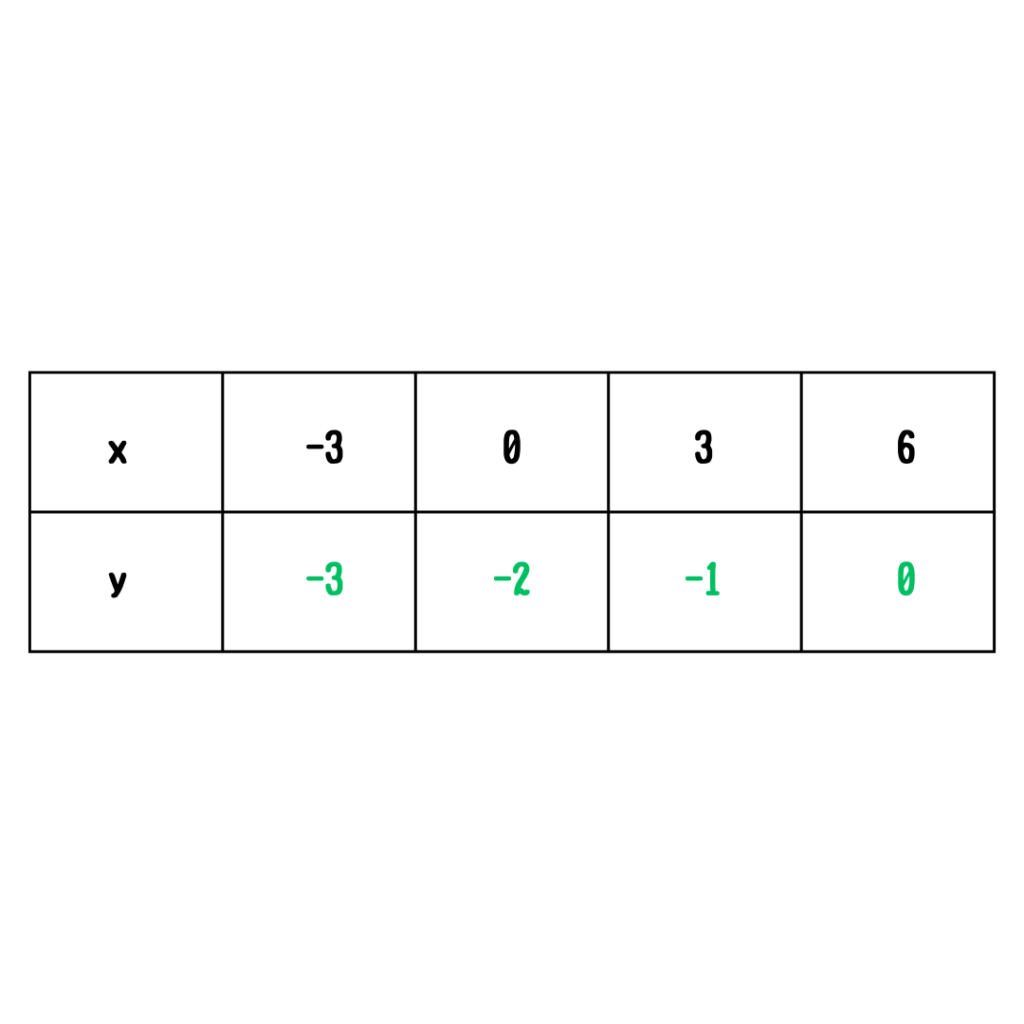
さっきの表の点をポイントしていこう。
\(x=-3のとき、y=-3\)
\(x=0のとき、y=-2\)
\(x=3のとき、y=-1\)
あとはポイントしたところを定規でシュッとすればOK！

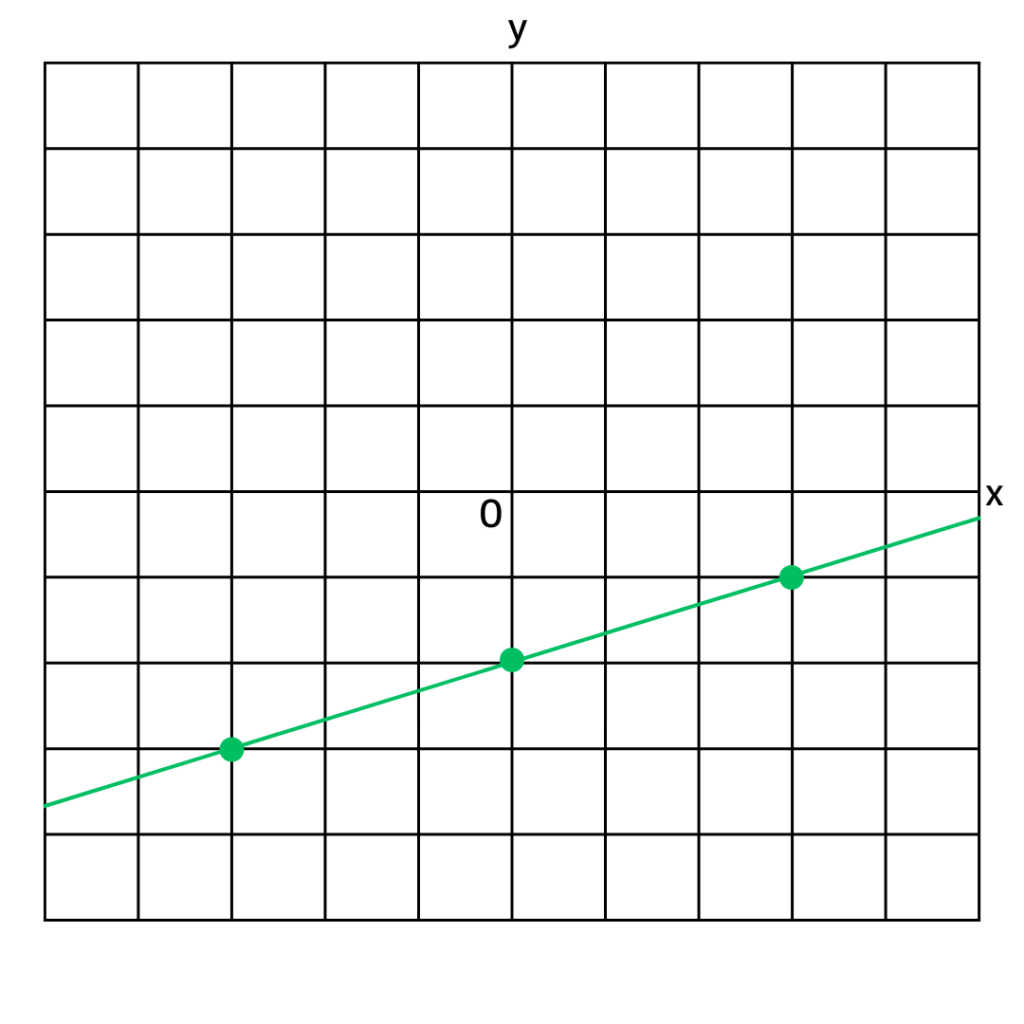
今回は、一次関数のグラフが通る点を
計算して出しました。
もう一つ、切片が分かってるときは、切片と傾きを
つかったグラフの書き方があります。
こっちは計算いらずです。

まずは切片の座標をとるよ。
切片は\(x=0\)なので、\(y軸上\)の値だよ。
だから\(y軸上の-2をポイントします。\)

次に傾きを見よう。
傾きは\(\frac{1}{3}\)、分数なので分母の数だけ右に動いて
分子の数だけプラスは上、マイナスだったら下
に移動しよう。
分数じゃなかったら、右に１動けばいいよ。
傾きの分だけプラスは上、マイナスだったら下
に移動しよう。
この問題は右に３、上に１動いたところに
ポイントしよう。
 この２点を通る直線を書けばかんぺき！
ただ、切片がグラフのマス範囲から外れているとか
分数の場合は切片がポイントできません！
なので、計算で通る２点を出してグラフを
かきましょう！

📝See an Example Problem【2】

2つの座標（-2,3）、（4,15）を通る一次関数を
式で表しなさい。
☝️ポイント1
\(一次関数を式で表すとか式を求めるって？\)
\(一次関数の式は　y=ax+bです\)
\(この式のaとbを数字にすること\)
これが一次関数を式で表すってこと！


✌️ポイント2
\(一次関数は、xとyの関係を「y = ax + b」の\)
\(形で表します。\)
そして、この２つの座標は必ずこの直線の上にあります。
つまり…
\(この2つの座標（-2,3）と（4,15）を
\) \(式「y = ax + b」に代入すれば\)
aとbを求めることができるよ。

では、やってみましょう！
\(まずは(-2,3)をy=ax+b入れてみよう。\)
\(x=-2,y=3だから\) \[3=-2a+b\] 文字が=の右にあるのは見慣れないよね。
＝の左右の場所だけ変えてしまおう！ \[-2a+b=3\]
\(次に、(4，15)をy=ax+b入れてみよう。\)
\(x=4,y=15だから\) \[15=4a+b\] 文字が=の右にあるのは見慣れないよね。
＝の左右の場所だけ変えてしまおう！ \[4a+b=15\]
この２つの式が両方成り立たないといけない。
だから、連立方程式で解いていきましょう！

まずは、それぞれの式に番号を振ろう。
\[-2a+b=3・・・①\] \[4a+b=15・・・②\]
これを連立させて
\begin{eqnarray} \left\{ \begin{array}{l} -2a+b=3・・・①\\ \:\:\:4a+b=15・・・② \end{array} \right. \end{eqnarray}
\(bがそろってるので②-①をするよ。\)
\begin{eqnarray} 4a + b & = & 15 \\ -) \:-2a + b & = & \:3\\ 6a\:\:\:\:\:\:\:\: & = & 12\\ a&=&2 \end{eqnarray}
②のほうがマイナスがない。
こっちの方が計算ミス減りそうだから
\(a=2を②へ代入。\)
\[4a+b=15・・・②\] \begin{eqnarray} 4\times2 + b & = & 15 \\ 8 + b & = & 15\\ b & = & 15-8\\ b & = & 7\\ \end{eqnarray} \(これでa=2,b=7なので、求める式は\)
 \[y=2x+7\]

こんな感じ！
２つ座標から、連立方程式でaとｂが出せるよ。
これで全部解ける！
だから、連立の計算は練習しておこう！

ひとりひとり理解のしかたもスピードも違うよね。
だから、今回とりあえず一回授業聞いてみるのも
全然ありだと思います。

一度体感してみてください！

お申し込み・お問い合わせはこちらから

【次回予告】

9月の数学ステップアップゼミ
9月27日(土)の予定です。
【中1の単元】　方程式の利用問題
【中2の単元】 1次関数の利用問題

ゼミの授業内容は、ITTO個別指導学院 長野の
ホームページにアップします！
またお目にかかること楽しみにしております✨

お知らせ,川中島校,篠ノ井校,青木島校中学生数学,長野市

Posted by itto-nagano