【2月】ステップアップゼミ数学
もうすぐ進級だね…

3学期期末テストで思った以上の成果が出なかった…

今のうちにわからない問題を解決しておきたい!
そんなとき…
ITTO個別指導学院 長野の
ステップアップゼミがあるよ✨
↓詳しくはこちら↓
数学ステップアップゼミ
2月は
2月21日(土)
開催!
学年なんて関係ない!
中学生なら必要な単元を選んで参加OK👍
2つとも参加もできるよ✨
🎈川中島校・青木島校🎈
中1の単元 13:00~13:50
中2の単元 14:00~14:50
🪄篠ノ井校🪄
中1の単元 13:00~13:50
中2の単元 16:00~16:50
★お申し込みは2月13日(金)まで!★
📝受講料📝
3,010円(税込み)
2月のステップアップゼミ【数学】
中1の単元
【空間図形の表面積と体積】
中2の単元
【場合の数と確率】
授業時間は50分
✨【とってもよくわかる解説(15分くらい)】
🖍️【問題を解く時間もたっぷり(20分くらい)】
🎉【やさしいポイント解説(15分くらい)】
2月【中1の単元】は
こんな感じの問題
📝See an Example Problem1
下図のような円錐の表面積を求めなさい。
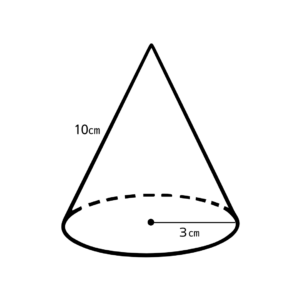
【👉ポイント】
円錐の表面積の求め方を考えよう💡
ここで類題。
母線が10㎝で底面の半径が2㎝の円錐の表面積
を考えてみる😀
☝️ステップ1
展開図を書いてみよう❗
そうすることで、面積を求める図形が見やすくなるよ✨
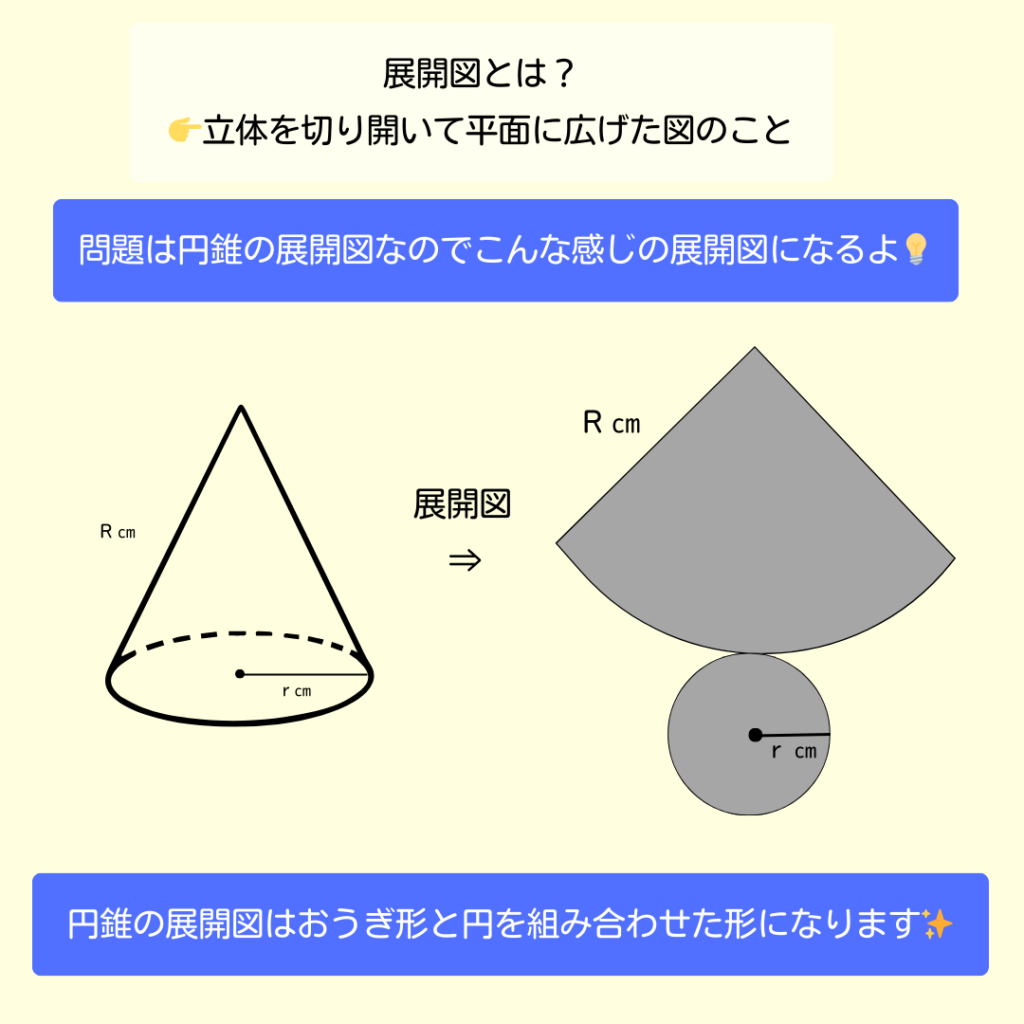
✌️ステップ2
展開図でできたおうぎ形の中心角を求めよう💡
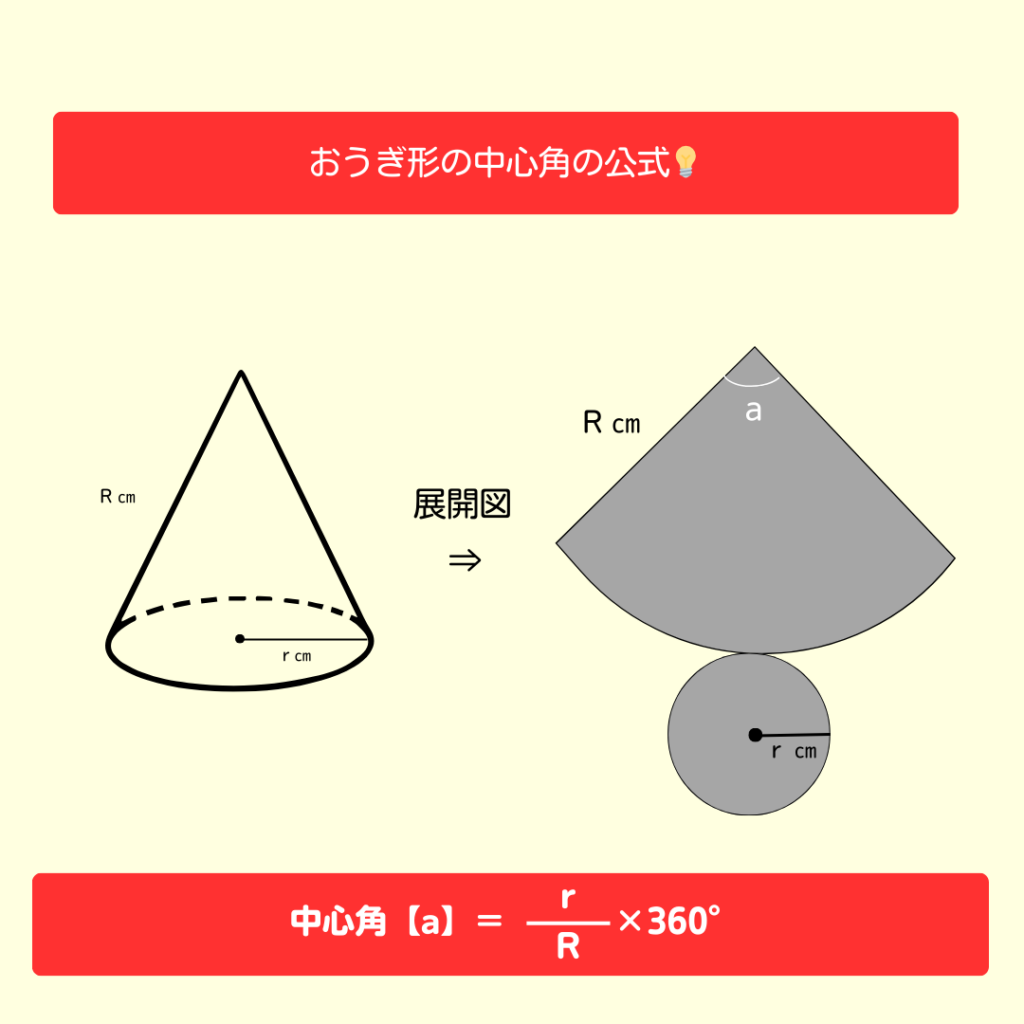
母線が10㎝で底面の半径が2㎝の円錐だから、
\[a=\frac{2}{10}\times360°=72°\] になるよ❗
じつは…円錐の場合は、
中心角がなくても、おうぎ形の面積は出せます❗
これはステップアップゼミで👍
👌ステップ3
円錐の表面積=おうぎ形の面積+円の面積
で求めよう💡
\[πR^2\times\frac{中心角}{360}\] 底面の円の面積は… \[πr^2\] になるよ!
なので例題は…
母線の長さが10㎝、底面の半径が2cm、中心角72°なので
\[10^2π\times\frac{72}{360}\] \[100π\times\frac{1}{5}=20π\] 底面の円の面積は… \[2^2π=4π\] だから \[\mathbf{20π+4π=24π㎠}\]
おし🙌では問題を解こう✍️
☝️まずは展開図から
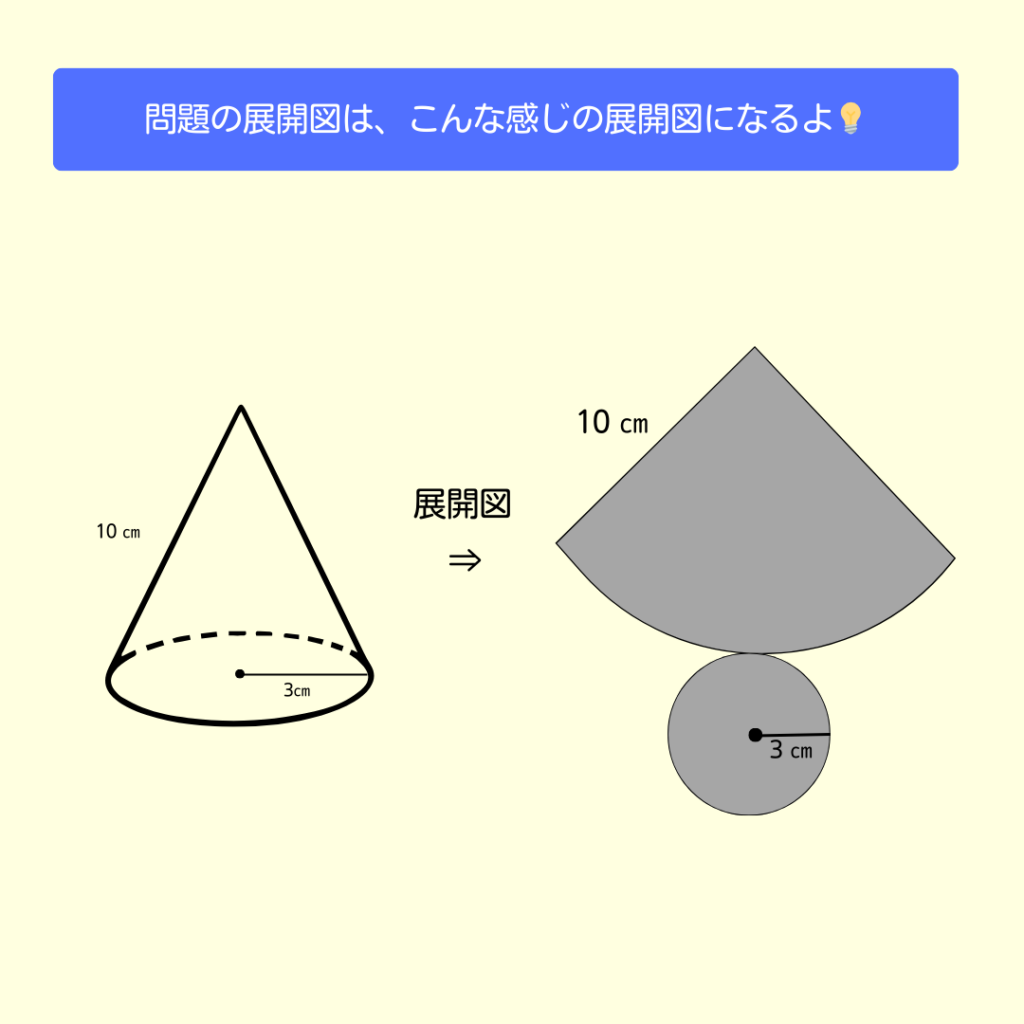
✌️展開図から、おうぎ形の中心角を求めてみよう
\[a=\frac{3}{10}\times360°=108°\] になるよ!
👌円錐の表面積=おうぎ形の面積+円の面積
で求めよう
よって \[30π+9π=\mathbf{39π㎠}\] でOK!
ここはどうしても公式とかの知識がいるから💦
そこはしっかり押さえておこう💡
📝See an Example Problem2
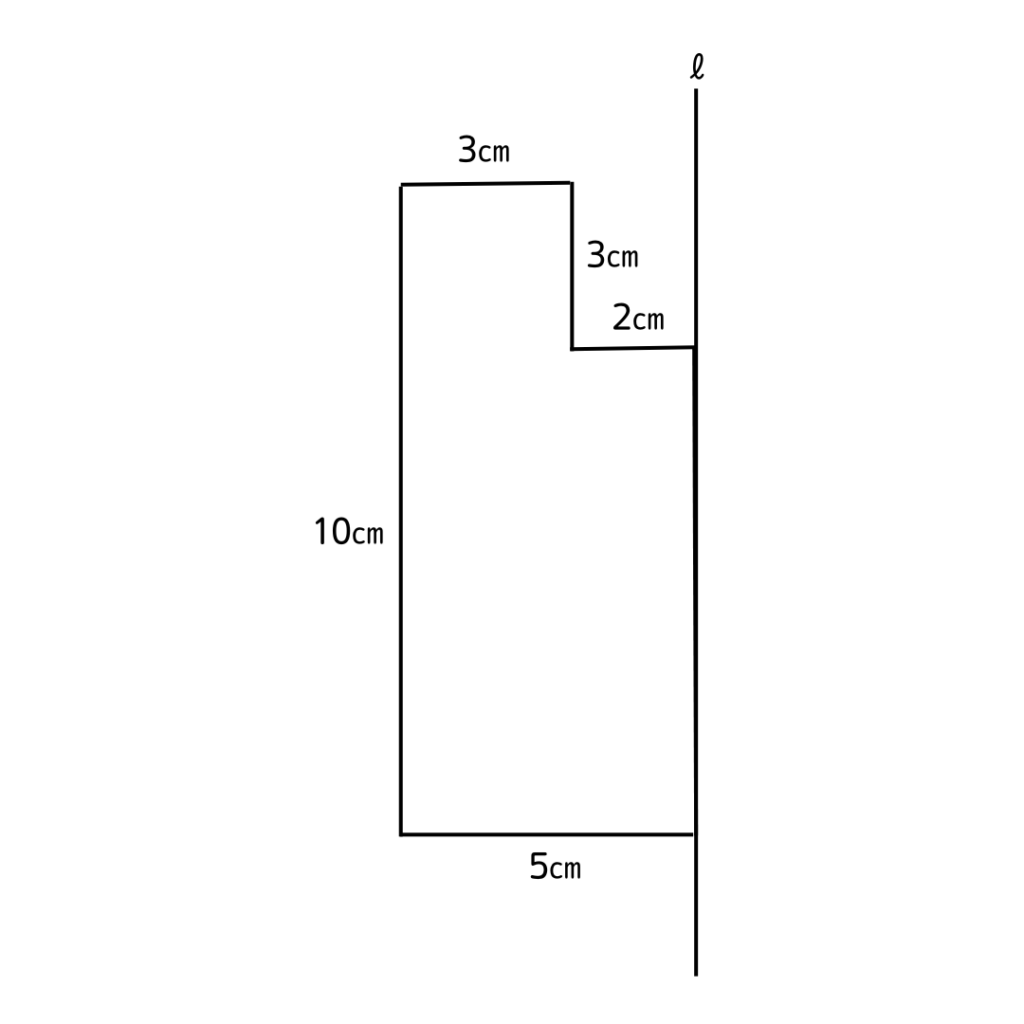
下の図のような図を直線ℓを回転の軸として
回転した時にできる立体の体積を求めなさい。
☝️ポイント1
回転の軸で1回転させたときの軌跡の見取り図を描いてみよう💡
こんな感じで考えてみよう🤔
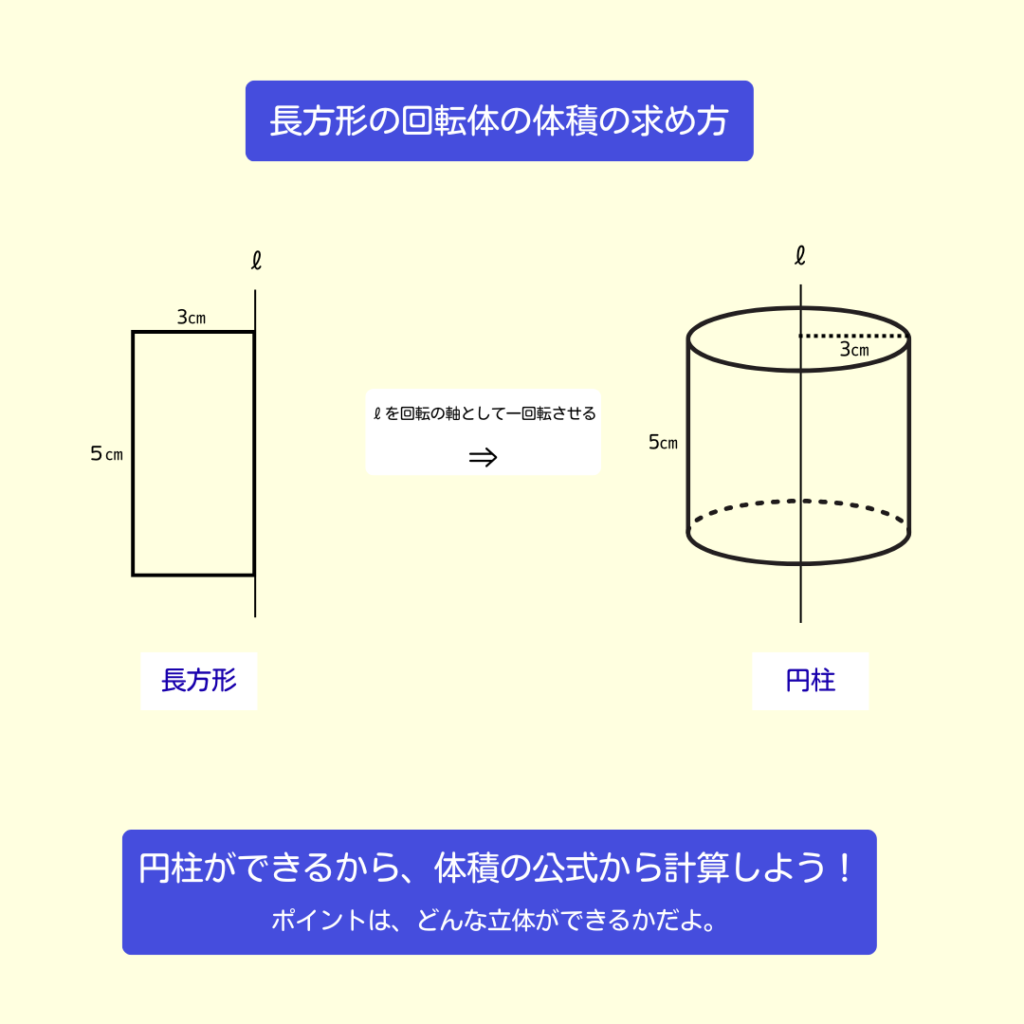
✌️ステップ2
この場合は回転させると円柱ができる💡
なので、円柱の体積で求めることができます✨
\[\large{底面積\times高さ}\] なので… \[3^2π\times5=45π㎤\] になるよ!
では問題に進もう✍️
☝️まずは回転させよう
そうすると…
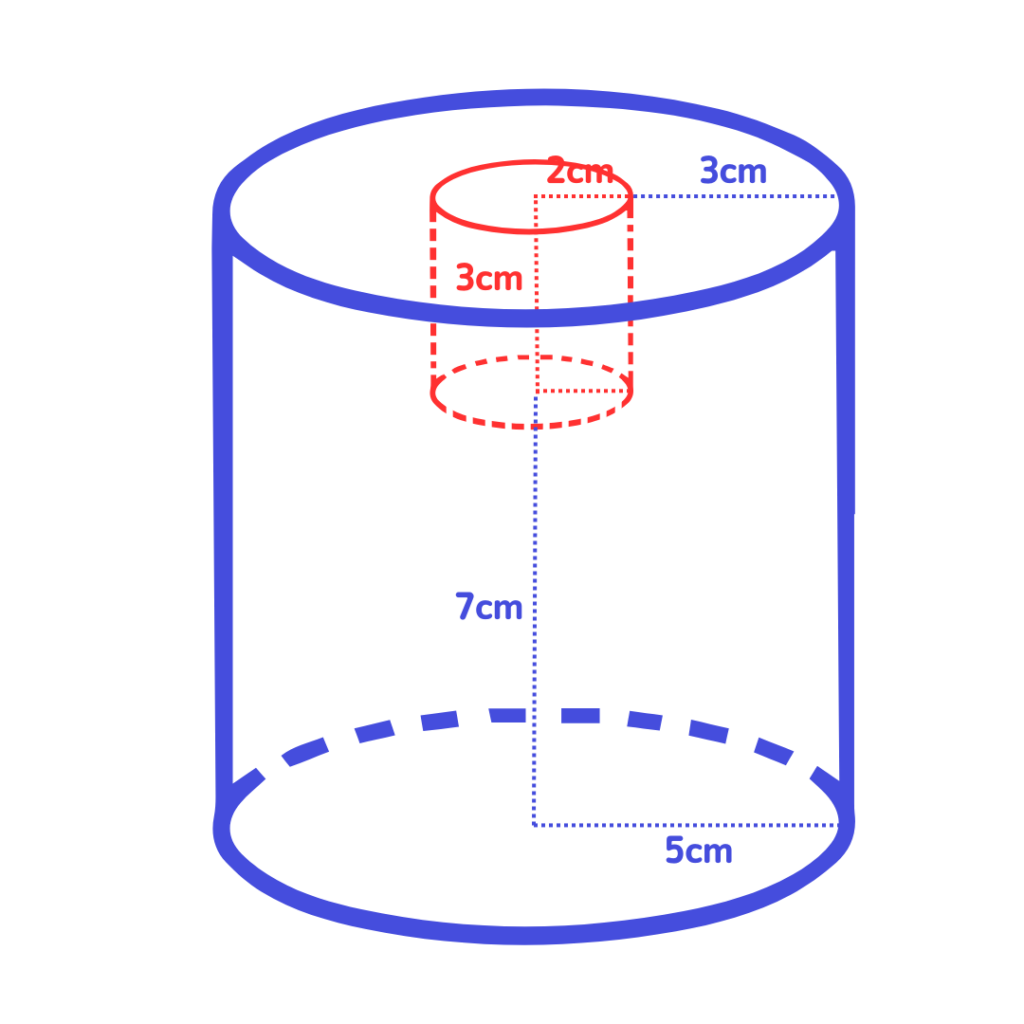
こんな感じの立体ができます💡
赤い円柱の部分が空洞になります💡
だから…
【青い円柱の体積】-【赤い円柱の体積】
でOK👍
\[5^2π\times10=\mathbf{250π㎤}\] 赤い円柱は底面の半径が2㎝で高さが3㎝なので
\[2^2π\times3=\mathbf{12π㎤}\] あとは、【青い円柱-赤い円柱】で \[250π-12π=\mathbf{238π㎤}\] こんな感じで解けるね👍
2月【中2の単元】は
こんな感じの問題
📝See an Example Problem1
4人の生徒A、B、C、Dさんを学校のリレーに選出します。
この4人の中から第1走者、第2走者、第3走者、第4走者を選ぶ場合、何通りできるかを求めなさい。
👍ポイント
もれなく数え上げれるかが勝負。
【順番】と【組み合わせの】の区別もしておこう💡
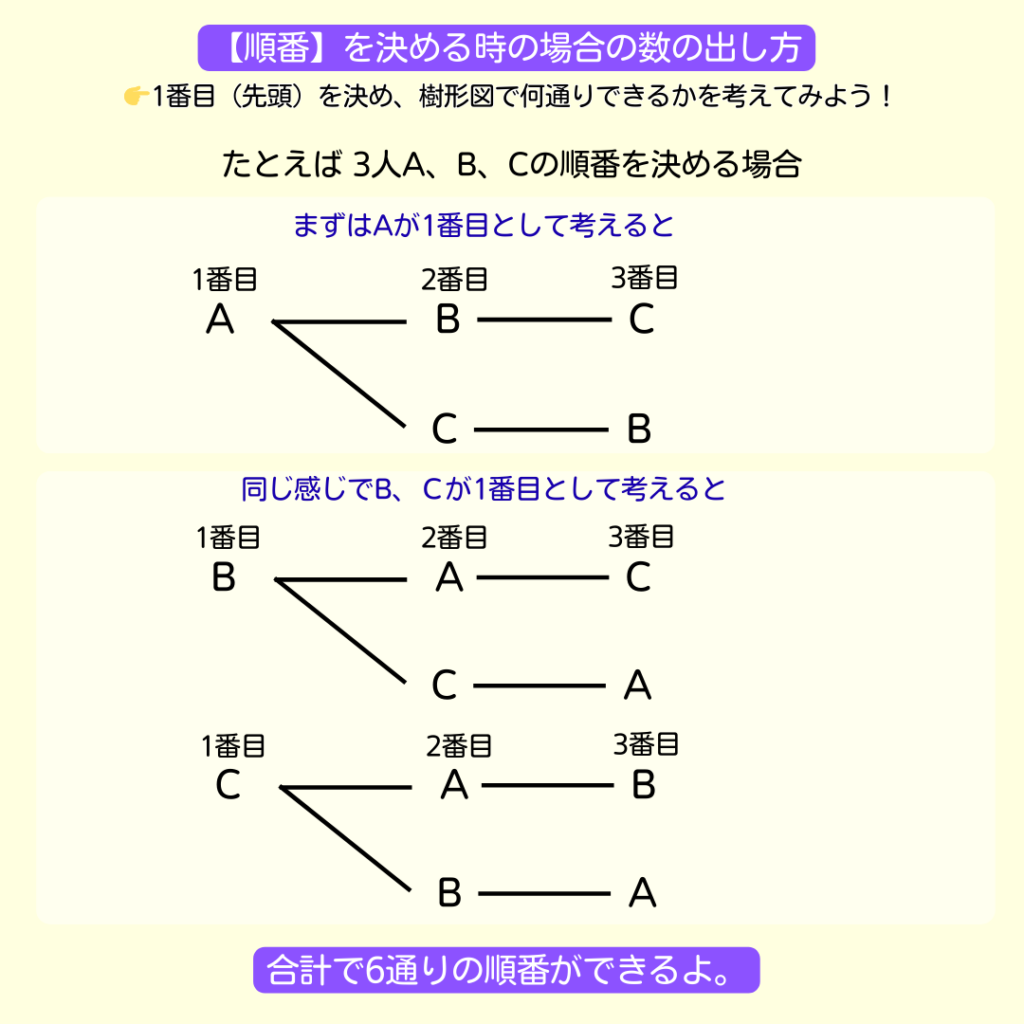
では、問題を解いていこう✍️
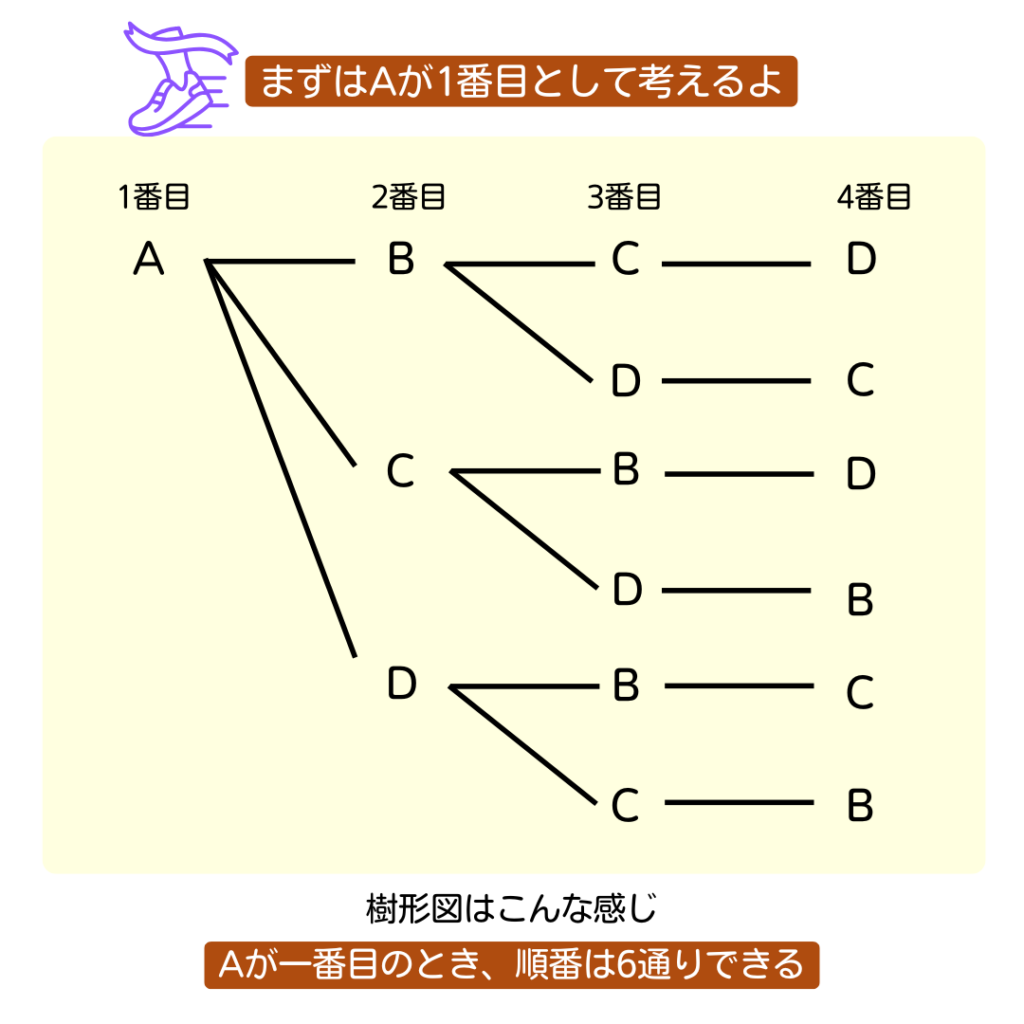
同じ感じで、B・C・Dが1番目として考えると…
それぞれ6通りできるから
合計で
6通り×4人=24通り
の順番だね👍
📝See an Example Problem2
3人で1回だけ、じゃんけんをします。
①1人だけの勝ちが決まる確率を求めなさい。
②負ける人が1人、もしくはいない確率を求めなさい。
👉ポイント
確率ってなに?
確率は、基本的には分数で表したものになるよ🤚
じゃんけんの組み合わせの場合は
表を使って全体で何組できるかをまず考えてみよう💡

このとき…
A君が勝つ組み合わせは3組・B君が勝つ組み合わせは3組
勝敗が決まる組み合わせは6組・あいこの組み合わせは3組だから
まずは①からいこう✍️
表を使って全体で何組できるかをまず考えてみよう✨
3人でじゃんけんをすると以下の27通りの組み合わせになるからね🙌
これは何度も出てくるから覚えておくと便利だね👍
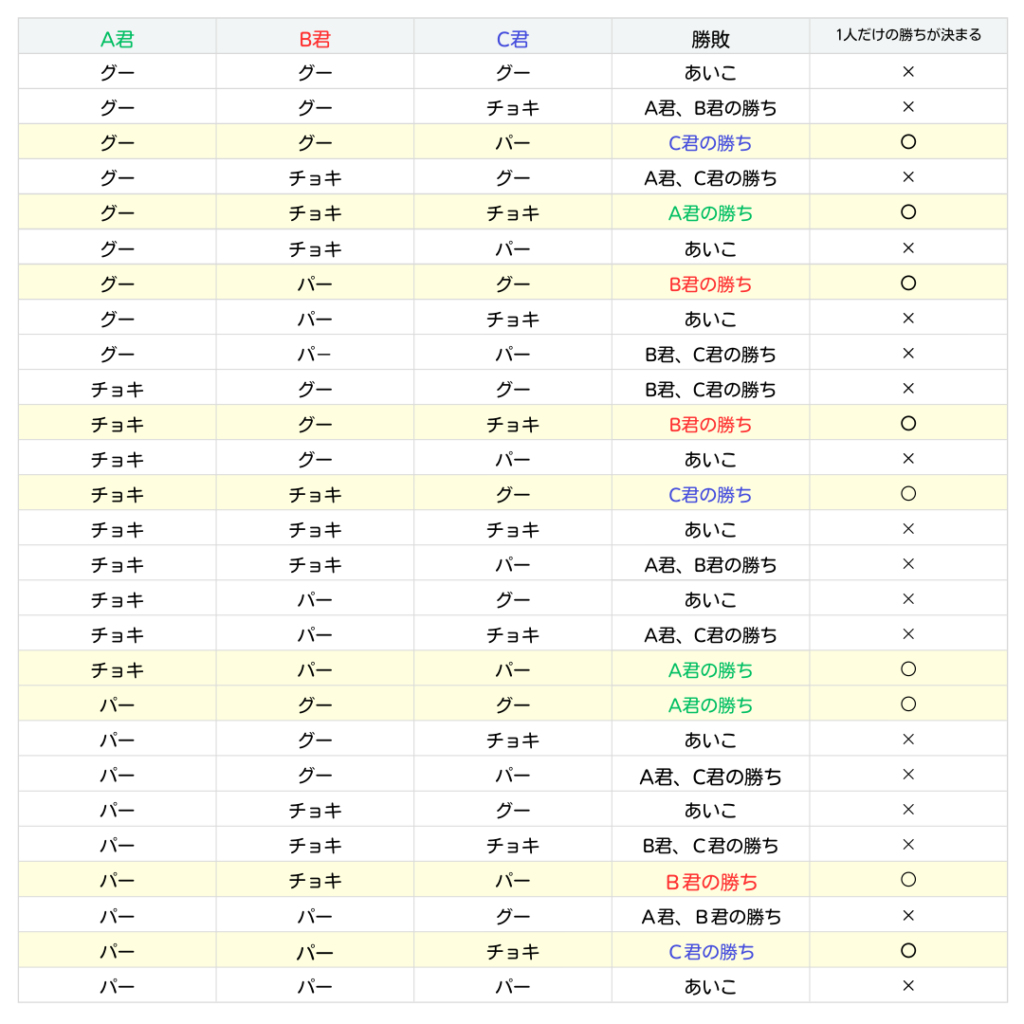
1人だけの勝ちが決まる場合の数は…
表で色をつけてある9通り💡
最後に②を解こう✍️
①で1回のじゃんけんで1人だけの勝ちが決まる場合
👉負ける人が2人いるってこと
問題文はそれ以外の場合を指しています💡
だから、確率は…
【起こり得るすべての場合の数】-【1人だけの勝ちが決まる場合の数】です。
だから…
27-9=18通り
あることになります。
今回はこんな感じのゼミ内容です👆
【3月のご案内】
次回のステップアップゼミ数学は…
3月21日(土)開催(予定)
【中1の単元】
データの活用
【中2の単元】
箱ひげ図
統計の単元だね。
知ってて損はない単元です👍
しっかり復習しておこう❗
ゼミの授業内容は、ITTO個別指導学院 長野の
ホームページにアップします❗
ITTO長野のホームページでは
学習にまつわるコンテンツを随時更新中🎉
またお目にかかること楽しみにしております✨








