※受付終了【10月】ステップアップゼミ数学
こんな声が聞こえる季節

また文字が出てきた…
マジでめんどくさい

先生の話…
早すぎて頭パンクするんだけど
そんなモヤモヤ…。
ITTO個別指導学院 長野の数学ステップゼミなら、
解決していけるかも✨
↓詳しくはこちら↓
数学ステップアップゼミ
10月は
10月25日(土)
開催!
学年なんて関係ない!
中学生なら必要な単元を選んで参加OK!
2つとも参加もできるよ!
🎈川中島校・青木島校🎈
中1の単元 13:00~13:00
中2の単元 14:00~14:50
🪄篠ノ井校🪄
中1の単元 13:00~13:50
中2の単元 16:00~16:50
★お申し込みは10月17日(金)まで!★
📝受講料📝
3,010円(税込み)
10月のゼミ内容はこちら
中1の単元
【比例・反比例とグラフ】
中2の単元
【角度、内角・外角の和】
授業時間は50分
✨【とってもよくわかる解説(15分くらい)】
🖍️【問題を解く時間もたっぷり(20分くらい)】
🎉【やさしいポイント解説(15分くらい)】
今回の中1の単元はこんな感じ
📝See an Example Problem1
\(\:x\:の値とそれに対応する\:y\:の値が次のとき、\)
\(\:y\:を\:x\:の式で表しなさい。\)
\(①x=5のとき、y=40\)
\(②x=6のとき、y=-3\)
【☝️ポイント1】
\[【\:\:y\:が\:x\:に比例するとは?\:\:】\]\[☆\:y\:が\:x\:に比例するとき、関数の式は\:y=ax\:になる\] \[この\:a\:は比例定数と呼ばれてます\]
では、解いていきましょう!
\(まずは\:y\:が\:x\:に比例するから…\) \[式は…\:y=ax\:\]
で、ここに代入するんだけど…
式を反対にして\(\:\:ax=y\:\:\)にした方が、計算ミスなくなるよ!
これに\(\:x=5\:と\:y=40\:\)を代入すると
\[5a=40\]
\[a=8\]
だから、式は…\[\:y=8x\:\]だね。
\(まずは\:y\:が\:x\:に比例するから…\) \[式は…\:y=ax\:\]
で、ここに代入するんだけど…
式を反対にして\(\:\:ax=y\:\:\)にした方が、計算ミスなくなるよ!
これに\(\:x=6\:と\:y=-3\:\)を代入すると
\[6a=-3\]
\[a=-\frac{1}{2}\]
だから、式は…\[\:y=-\frac{1}{2}x\:\]だね。
こんな感じでできるよ!
📝See an Example Problem2
\(\:x\:の値とそれに対応する\:y\:の値が次のとき、\)
\(\:y\:を\:x\:の式で表しなさい。\)
\(③x=5のとき、y=4\)
\(④x=-3のとき、y=4\)
【✌️ポイント2】
\[【\:\:y\:が\:x\:に反比例するとは?\:\:】\]\[☆\:y\:が\:x\:に反比例するとき、関数の式は\:y=\frac{a}{x}\:になる\] \[この\:a\:は比例定数と呼ばれてます\]
\[☆比例定数を出すには、\:xy=a\:を使うと便利!\] \[つまり…\]\[\:x\:\times\:y\:をすると比例定数になってるよ!\]
では、問題解いていきましょうか。
\(まずは\:y\:が\:x\:に反比例するから…\) \[式は…\:y=\frac{a}{x}\:\]
で、\(\:a\:\)は\(\:x\times y\:\)で出せるから…
\[\:\:a=5\times4=20\:\:\]
\[a=20\]
だから、式は…\[\:y=\frac{20}{x}\:\]だね。
\(まずは\:y\:が\:x\:に反比例するから…\) \[式は…\:y=\frac{a}{x}\:\]
で、\(\:a\:\)は\(\:x\times y\:\)で出せるから…
\[\:\:a=-3\times4=-12\:\:\]
\[a=-12\]
だから、式は…\[\:y=-\frac{12}{x}\:\]だね。
今回の中2の単元はこんな感じ
📝See an Example Problem1
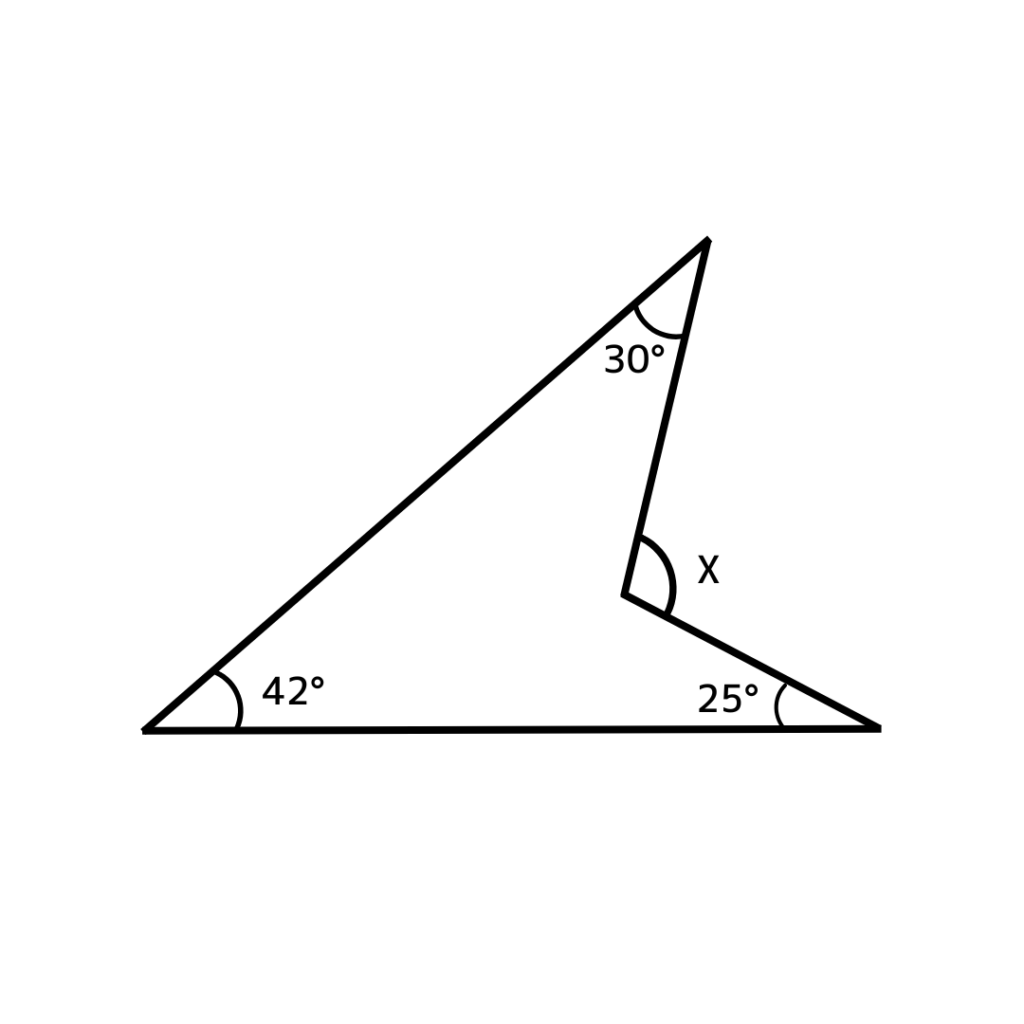
☝️【ポイント1】
三角形の性質を使おう!
では、実際に解いてみましょう!
このまま見ててもなかなか解けない…
だから三角形を2つ作るように線をいれてみるのがコツ!
その図がこれ!
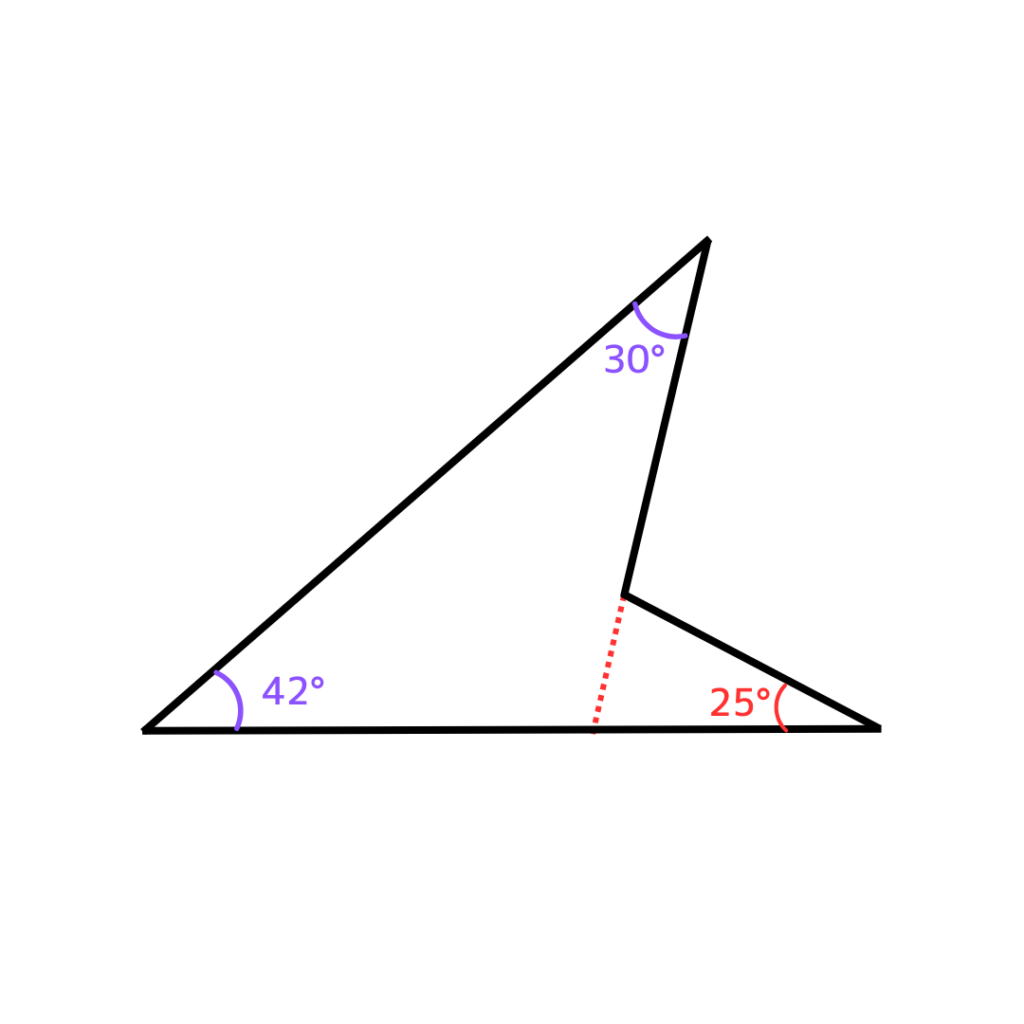
そうすると入れた点線の左と右に三角形が
ひとつずつできる。
左側の三角形から【ポイント】を使って
外角を計算してみよう!
図で求めた角度を確認してみよう!
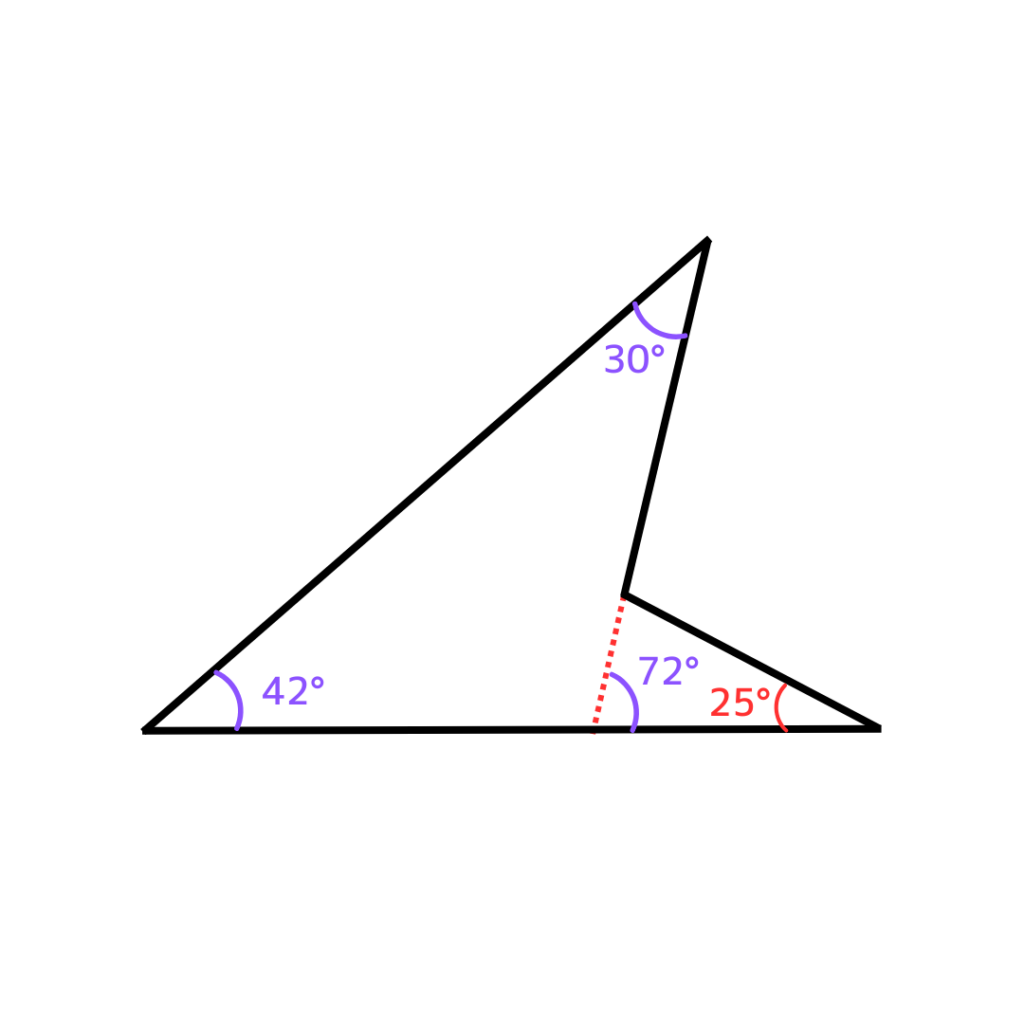
次に、右側の三角形から【ポイント】を使って
外角を計算してみよう!
図で求めた角度を確認してみよう!
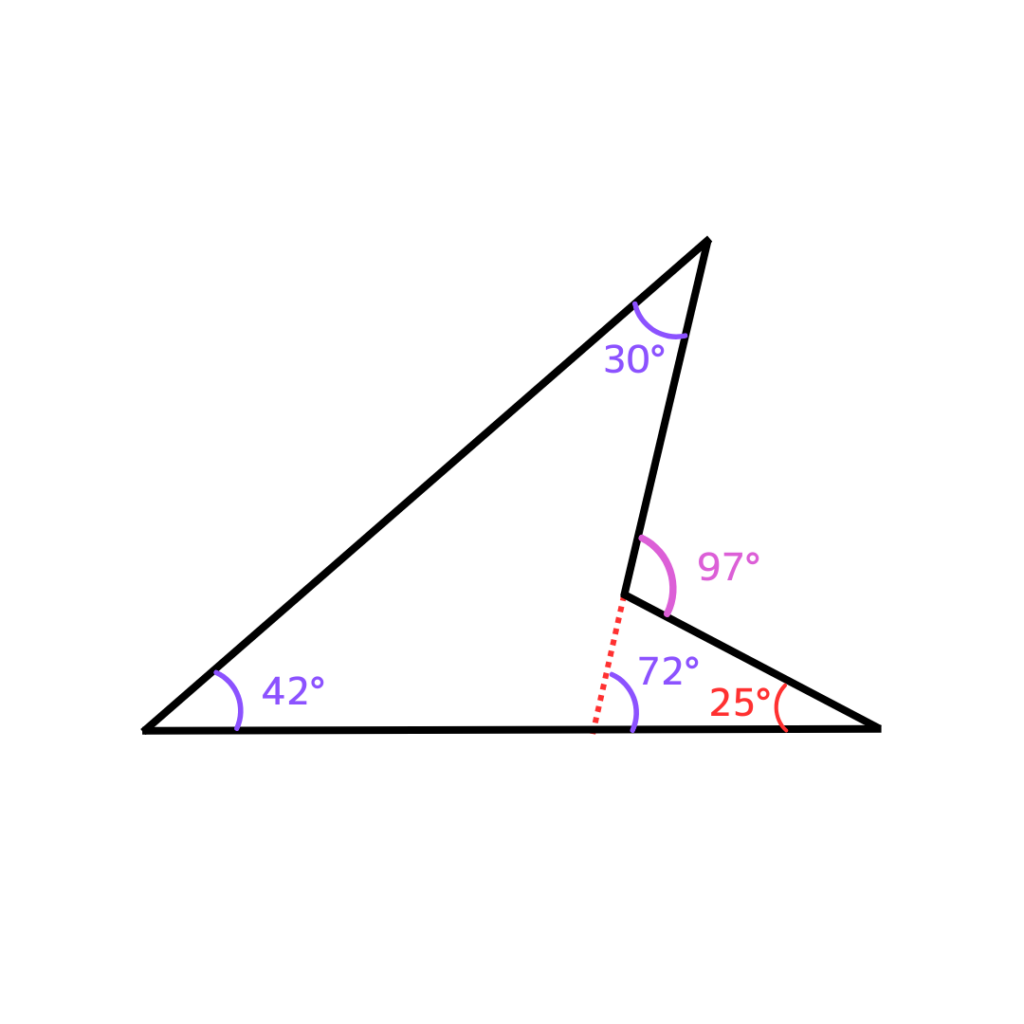
て感じで答えが出せる。
答えは97°だね。
これが一般的な考え方。
で、ここからは簡単な考え方。
この問題みたいな矢印みたいな形のものは…
図形のなかの角度を全部たすと
くぼんだ部分の角度になるよ!
実際計算してみると…
ほらね。
これ一つ覚えておくとこういうのは簡単に解けちゃうよ。
📝See an Example Problem2
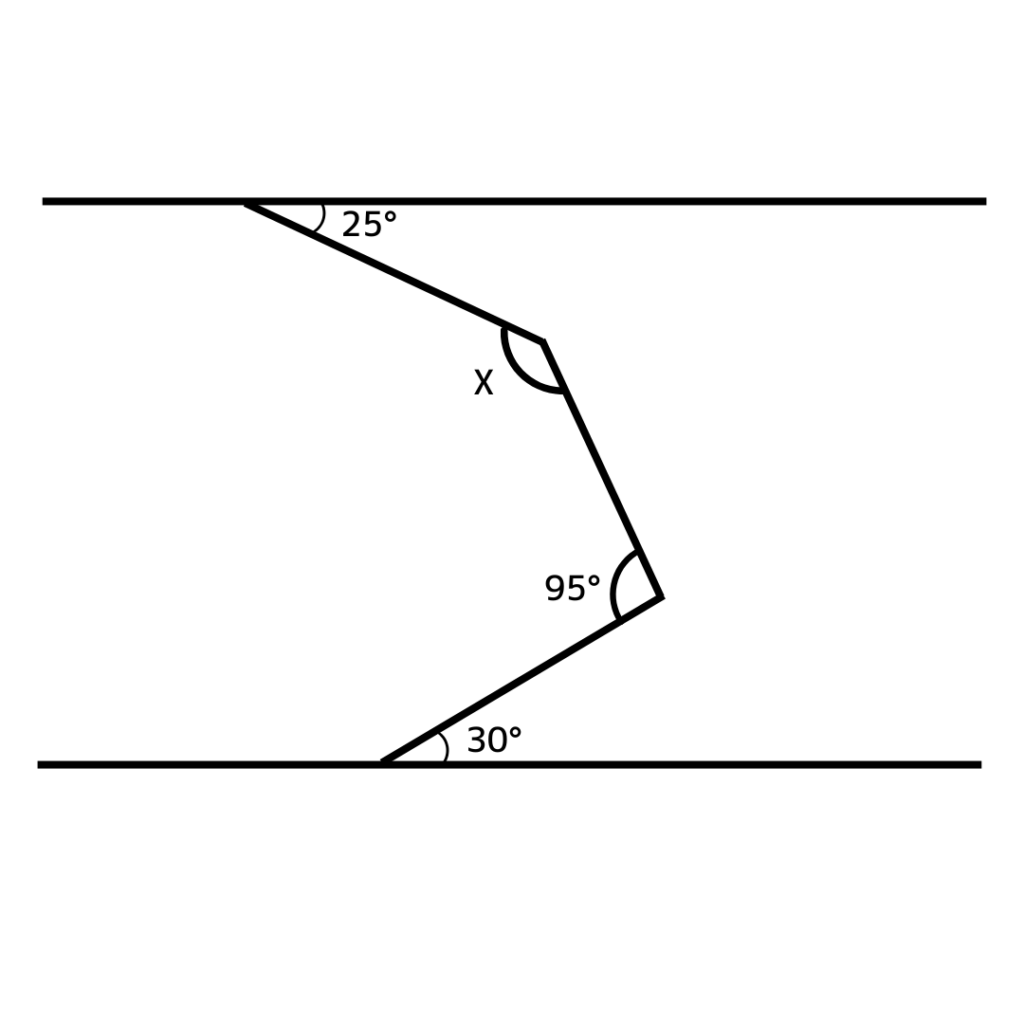
✌️【ポイント2】
平行線があれば同位角・錯角は等しい!
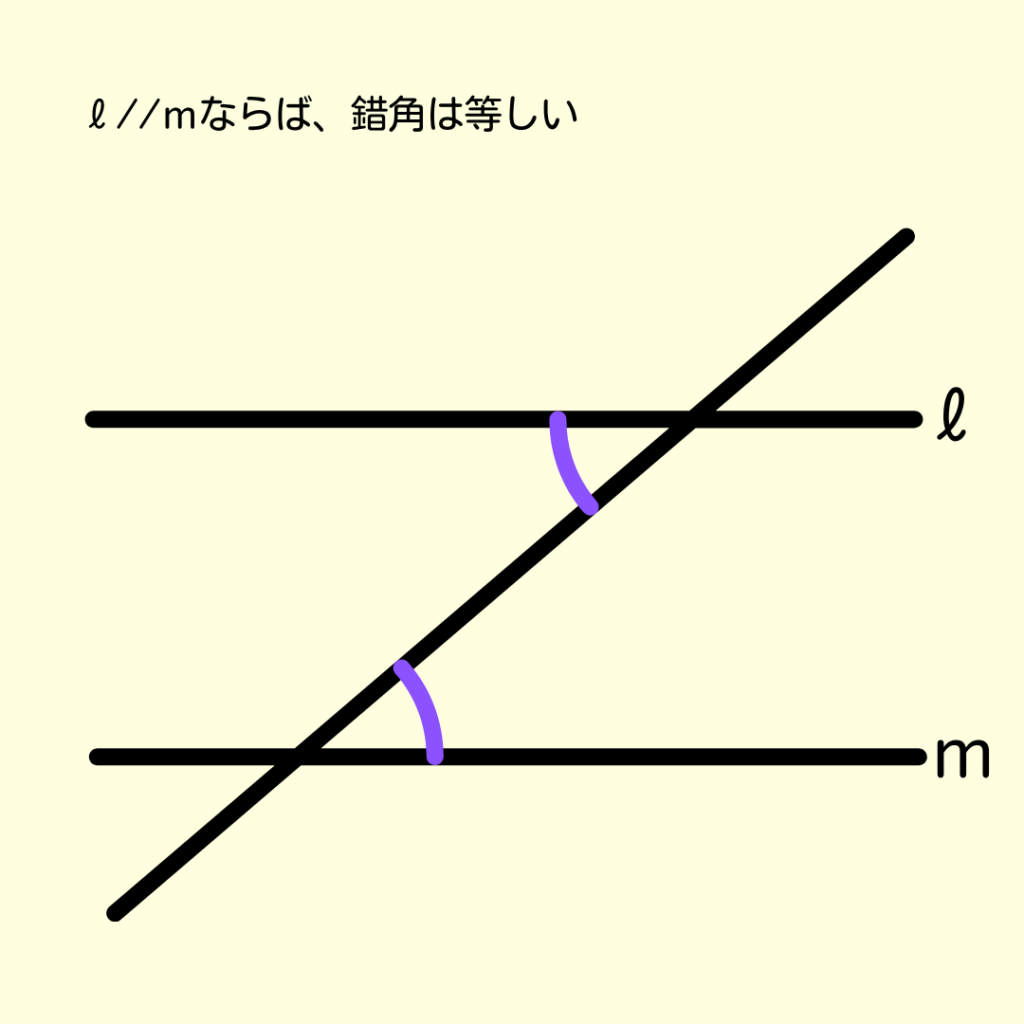
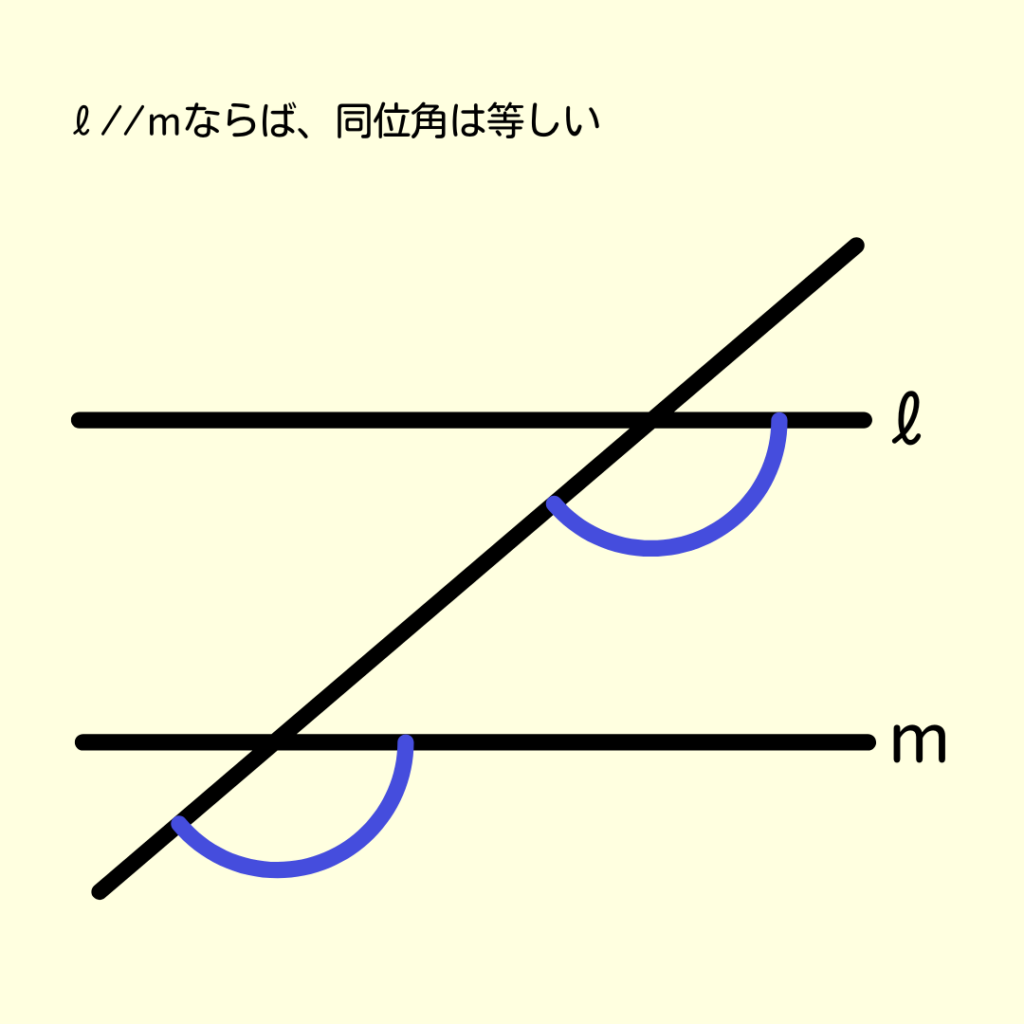
では、問題を進めてみよう!
こういう問題は平行線を入れてみるのがポイント。
図みたいな感じ
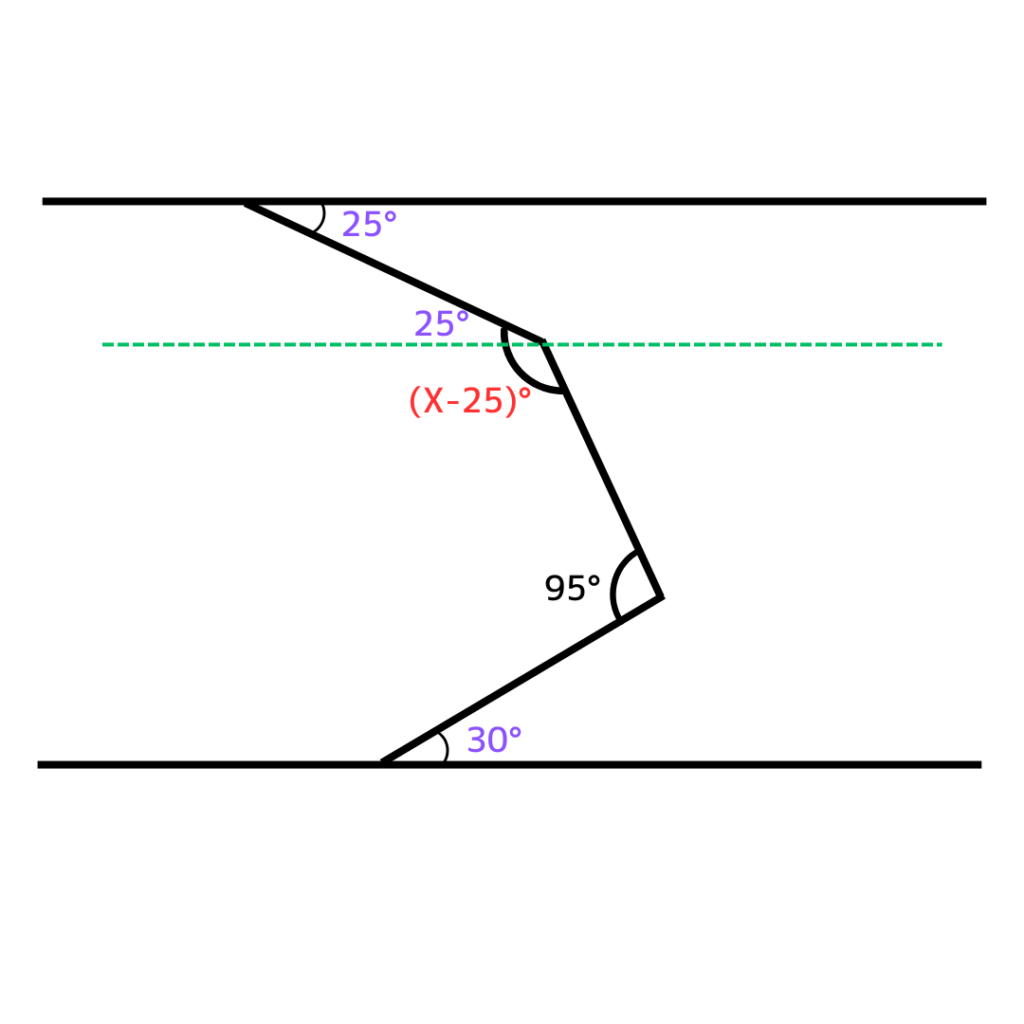
そうすると上の2本の直線で錯角ができます。
これで
ってなるよ。
下の方にも直線を入れてみよう!
こんな感じ。
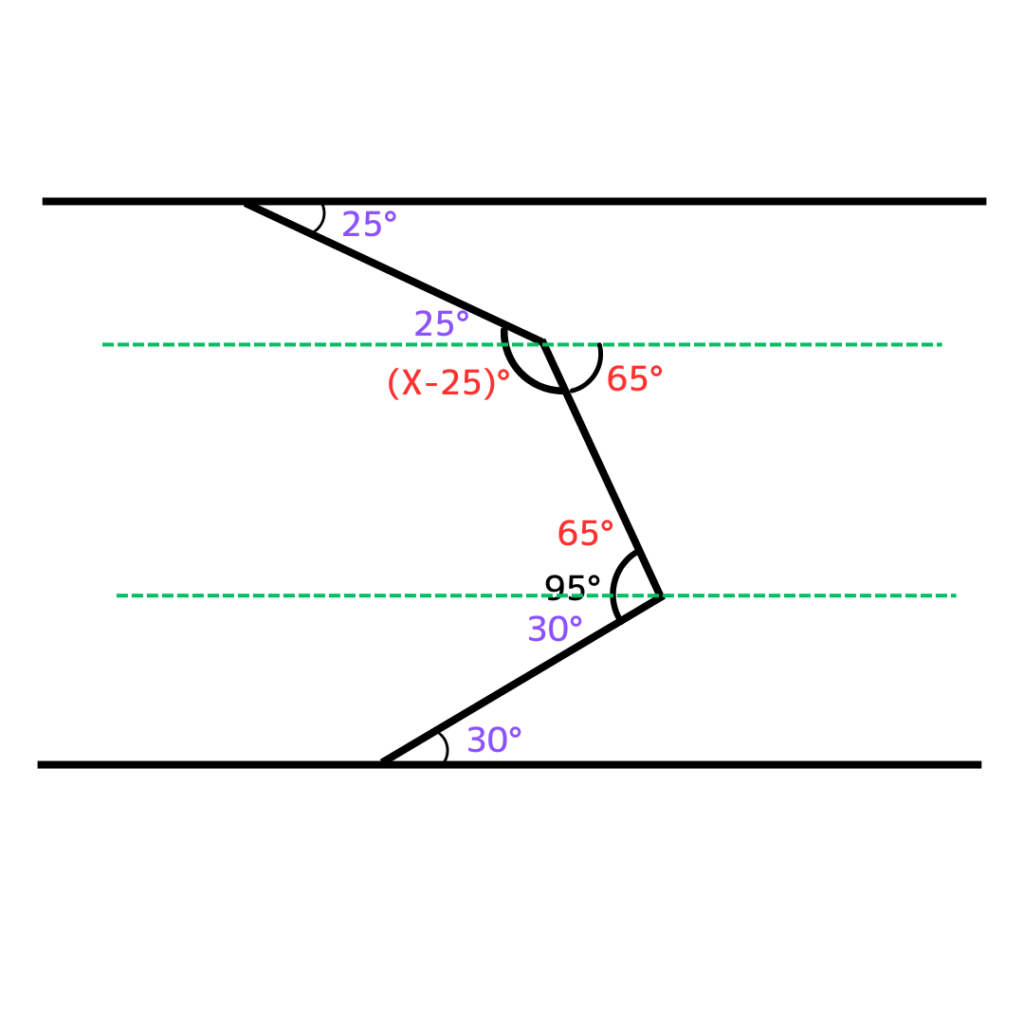
今度は下の2本で錯角ができます。
そうすると
ってなるよ。
さらに真ん中の2本を使って、錯角が見えます。
また、上の緑の点線の下部に180°があるね。
つまり、赤い角度の2つをたすと180°になるってこと.
だから、
だから答えは140°だね。
平行線の問題は錯角や同位角・また対頂角をうまく発見
できるかがポイントになるよ!
📝See an Example Problem3
🤟【ポイント3】
多角形の内角の和と外角の和を確認しよう!
→\(nは7ってことだから…\)
\[180(7-2)=180\times5=900\] だから、内角の和は900°って求められるよ!
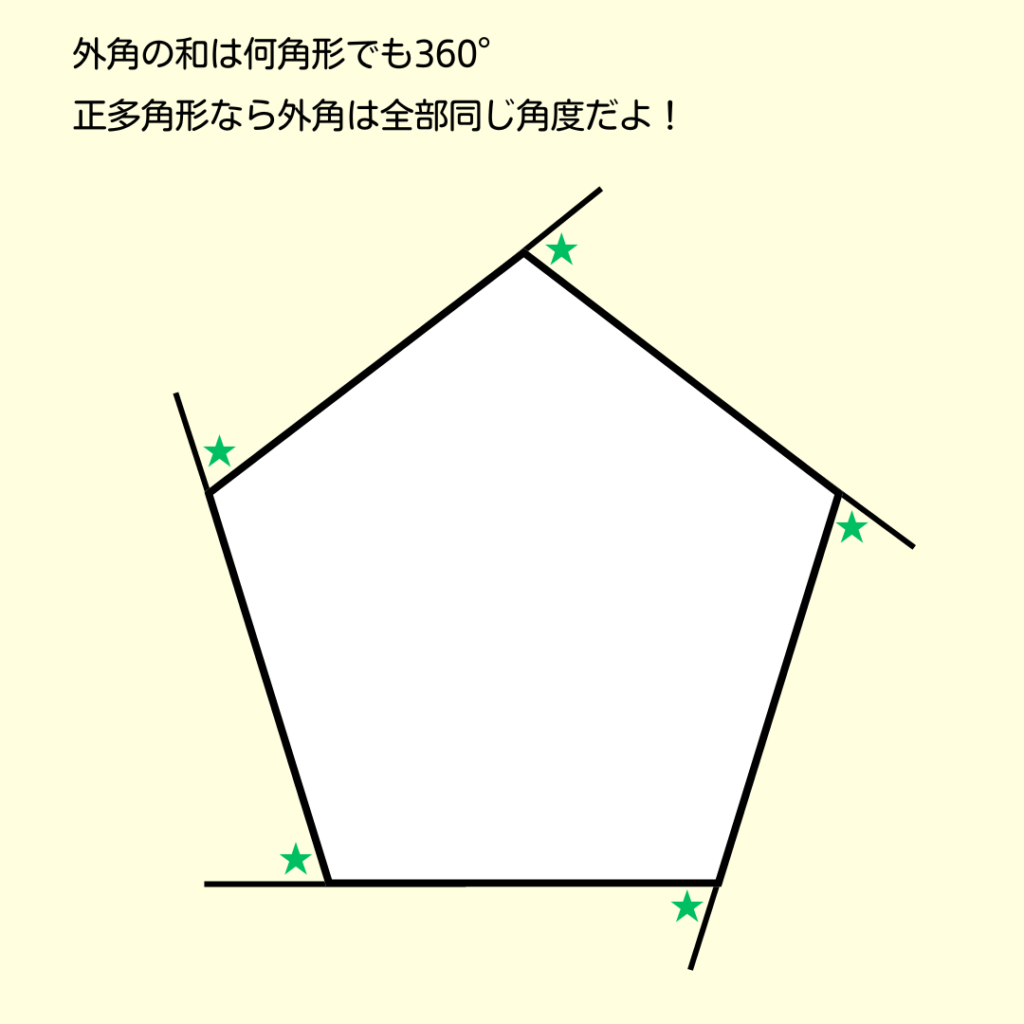
\[☆\:\:多角形の外角の和は必ず360°\] 正多角形なら、外角は全て同じだよ。
例えば、正五角形なら
\[360\div5=72\] だから、一つの外角は72°って分かるよ。
また、となりあう1つの内角と外角の和は180°になるからね
では、解いていきましょう!
ポイント3の知識を使うよ。 \[\:\:n角形の内角の和=180(n-2)°\] なので、八角形だったら
→\(nは8ってことだから…\)
\[180(8-2)=180\times6=1080\] だから、内角の和は1080°が答えだね。
次に、ひとつの内角を考えてみよう!
\[多角形の外角の和は必ず360°\] 正八多角形なら、外角は全て同じだから…
\[360\div8=45\] だから、一つの外角は45°。
内角と外角をたすと180°だから…
\[180-45=135\] つまり、答えは135°だね。
内角の和が分かってれば、それを角形数でわってもできるね。
\(1080\div 8=135\)
どちらでも出せるようにしておかないと対応できない問題もあるからね。
【次回のご案内】
11月の数学ステップアップゼミ
11月22日(土)予定です。
【中1単元】 比例・反比例の利用問題
【中2単元】 三角形の性質、合同証明
ゼミの授業内容は、ITTO個別指導学院 長野の
ホームページにアップします!
またお目にかかること楽しみにしております✨








