【篠ノ井校】2学期中間テストの解き方:中2数学
こんな問題を解いてみよう!
次の①~⑥の一次関数について(1)~(4)のそれぞれにあてはまるものをすべて選び、記号で答えなさい。
②\(\:\:y=2x-4\:\:\:\:\:\)
③\(\:\:y=\dfrac{1}{2}x+7\:\:\:\:\:\)
④\(\:\:y=-2x+3\:\:\:\:\)
⑤\(\:\:y=-\dfrac{2}{3}x-7\:\:\:\:\)
⑥\(\:\:y=\dfrac{1}{2}x-2\)
-1-300x300.png)
うーん💦グラフが右下がり😫
これって見た目で分かったりする😫
計算が必要になるの😖
みなと先生、教えてくれる❓
-300x300.png)
OK👍
答えは見た目で分かるよ😁
\(\:y=ax+b\:の\:a\:の数字を見てみよう!\)
\(この\:a\:の数字は傾きって呼ばれてるよ\)
→右上がりのグラフ
この傾きの数字がマイナス
→右下がりのグラフ
つまり…
\(\:x\:の前の数字を見れば分かるってこと\)
では、はるさんやってみましょう📝
-1-300x300.png)
そうなんだ💡
分数とかも関係ないなら…
④\(\:y=-2x+3\:\:\:\:\)
⑤\(\:y=-\dfrac{2}{3}x-7\:\)
かな。
みなと先生、あってる?
-300x300.png)
正解✨すばらしい👏
グラフの右下がりや右上がりは見た目だけで分かるよ。
知識だけはしっかりいれておこう❗
-1-300x300.png)
通る点が分かってるってことだよね…。
ってことは…
それぞれの一次関数の式に入れて式がちゃんとしてればいいってことだよね?
みなと先生、この考え方でよい?
-300x300.png)
そうその通り。
【グラフが\(点(12,-15)\)を通る】は…式に
\(【x=12を代入して計算するとy=-15になる】\)
と同じ。
では、はるさん
実際に①~⑥の式に\(x=12\)を代入して、\(y=-15\)になるものを見つけてみよう!
-1-300x300.png)
うん。やってみる。
まずは①から
だから、これはOKだね!
次に②から④までやってみよう
\[y=2\times12-4\] \[y=20\] これは違うね…。
③\(y=\dfrac{1}{2}x+7\)
\[y=\dfrac{1}{2}\times12+7\] \[y=13\] これも違う…。
④\(y=-2x+3\) \[y=-2\times12+3\] \[y=-21\] あー、これもダメだね。
最後に⑤と⑥
⑥\(y=\dfrac{1}{2}x-2\) \[y=\dfrac{1}{2}\times12-2\] \[y=4\] うーん。違うね…。
だから、答えは①と⑥だね。
みなと先生、どうでしょう?
-300x300.png)
Amazing🎉すばらしい👍
計算しっかりできれば得点になるよ✨
こんな感じで解いてみよう❗
\(あるもの\)
-300x300.png)
ハイ💦きた。増加量…💦
はるさん、一次関数で増加量って何を思い浮かべる❓
-1-300x300.png)
増加量?
たしか変化の割合ってやつじゃない?
-300x300.png)
OK👏
では、はるさん。
変化の割合って何だったっけ🤔
さらに…。
変化の割合の別名って知ってる❓
-1-300x300.png)
変化の割合はたしか…
別名は、たしか【傾き】だったから…
-300x300.png)
すばらしい👏
では、その知識を使って、ここで問題に戻ろう👍
はるさん、続きをお願いします✍️
-1-300x300.png)
はーい🤚
だから、\(【傾き】が\frac{1}{2}になってるものっと\)…
みなと先生、どうですか❓
-300x300.png)
正解🎉すばらしい👏
ここもそんなに計算いらないからね💡
一次関数の部分は、知識だけでけっこう解けるものもあるから。
一度しっかり復習しておくといいかな💡
-1-300x300.png)
はっ💬問題がいみふ-😰
先生、どうすればいいの?
-300x300.png)
OK👏
では、このグラフを簡単な図にしてみよう!
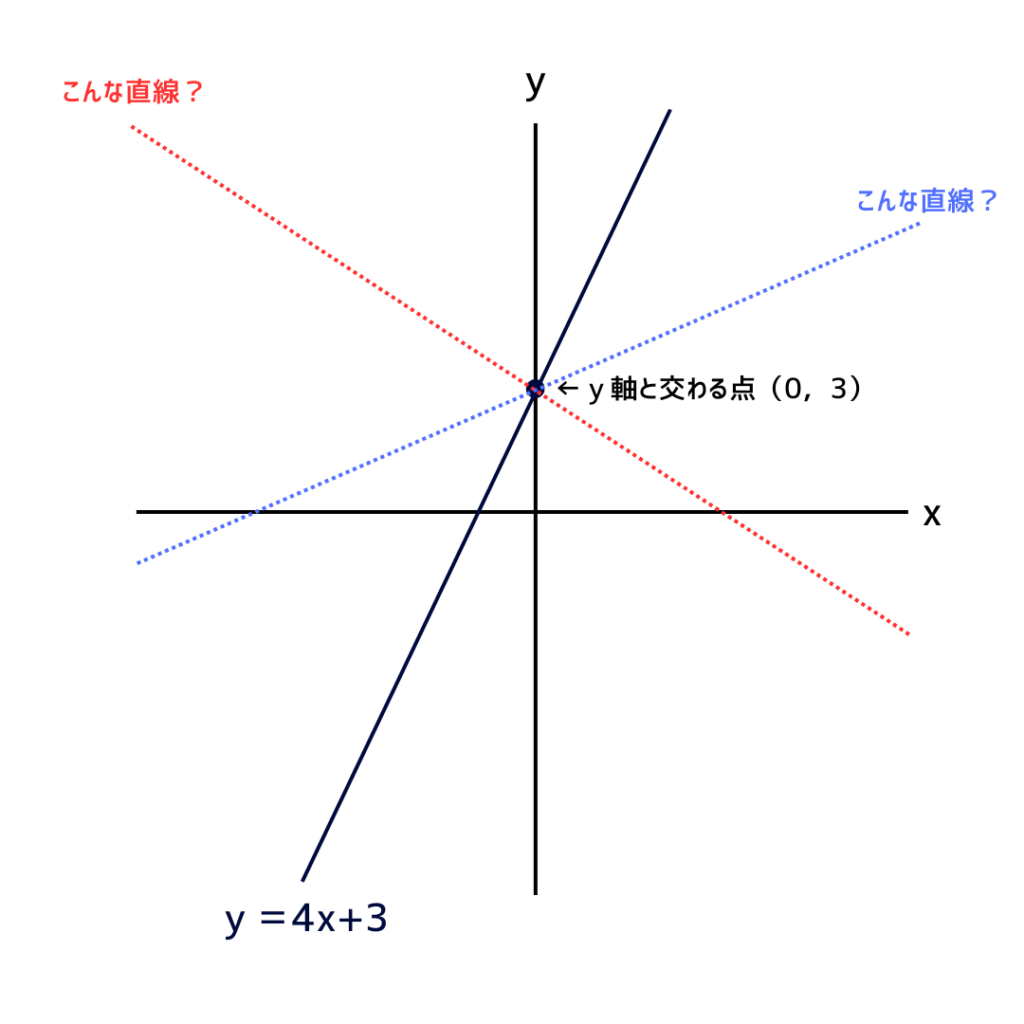
こんな感じかな。
この\(\:a\:の部分を傾き、\:b\:の部分は切片\)って
名前がついてるよ。
で、この切片がグラフと\(\:y\:軸\)と交わる点の\(\:y\:座標\)になってるよ。
だから…
はるさん、どういうグラフが答えの候補になるかな?
-1-300x300.png)
そっか❗
\(\:y=4x+3\:と切片が同じ数字(+3)を選べば\) \(いいってことか\)そうすると…
-300x300.png)
すばらしい👏
ここも知識で解ける問題になってるよ。
くどいけど、一次関数は知識があれば解けるから。
しっかり知識入れておきましょう✨
ITTO個別指導学院長野では、こんな感じで授業を進めていくよ。
お話しながら、解答をしっかり導けるように過程を大事にしています。
文字だけだと伝わらない部分って多いもの…
実際に体験してみて、お話してください。
みなさん、お待ちしています!







